A pendulum is released from rest from horizontal position as shown. The tangential acceleration when the pendulum reacheda t lowest when the pendulum reached at lowest position on its path is

zero
20ms−2
10ms−2
15ms−2
At lowest position tension and mg are present in vertical direction So that tangtential acceleration will be zero.
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform thin rod is released from rest in the horizontal position as shown in the figure. For what value of x, the angular acceleration is maximum.
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
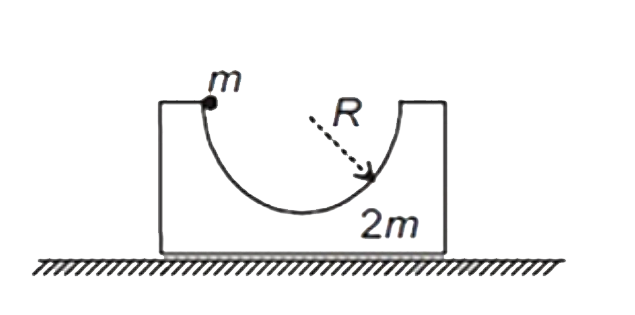
View Solution
Knowledge Check
A pendulum bob 'm' is released from rest from horizontal position as shown in the figure. ltbr> Choose the position where the chance of. Braking of the string is maximum.
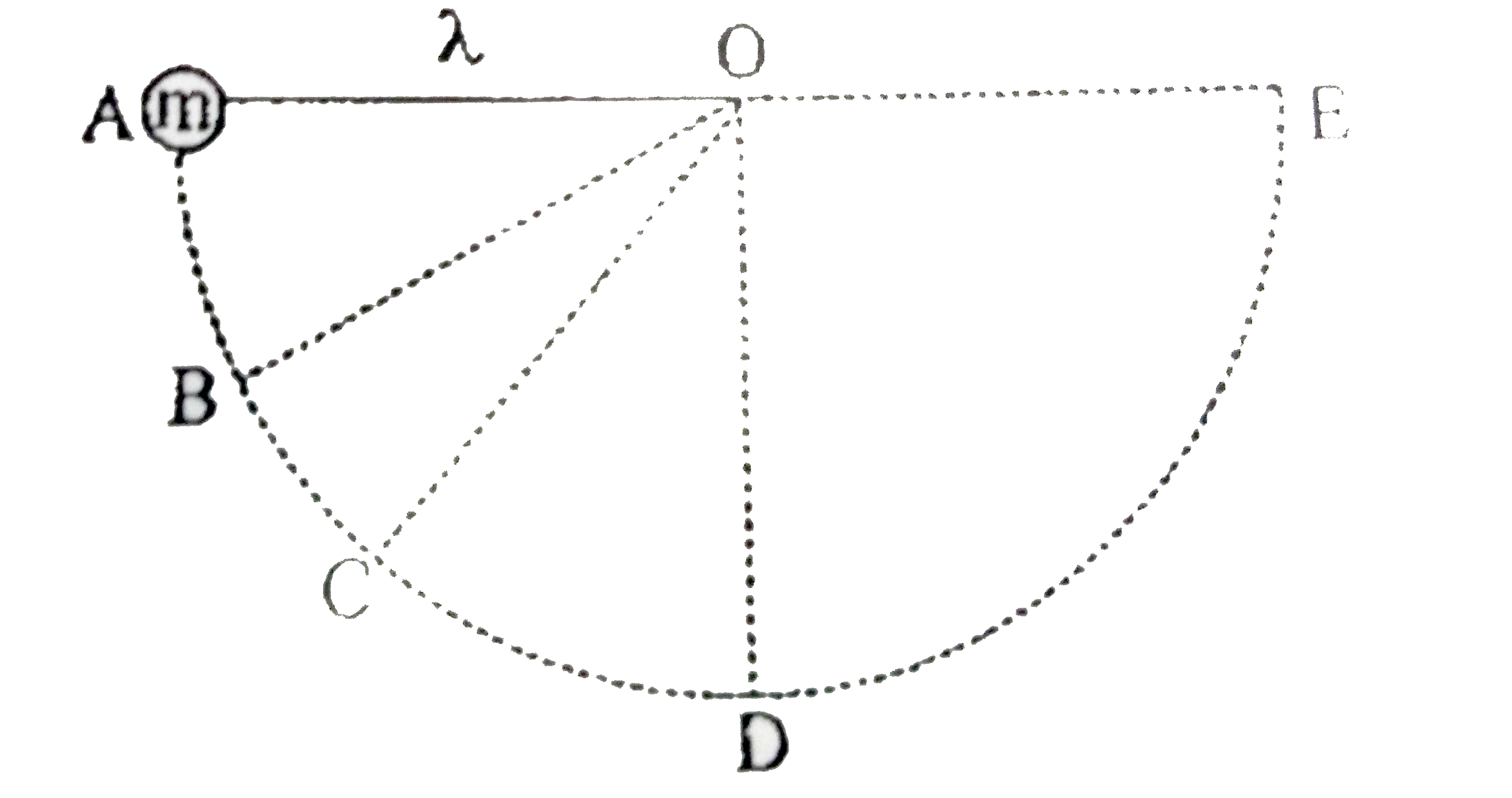 AABBCCDD
AABBCCDDA simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle θ with the vertical, the angle θ which the acceleration vector of the bob makes with the string is given by–
 Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2
Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2A simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
Aπ4Bcos−1(1√3)Csin−1(1√3)Dπ3
In the situation shown, a pendulum bob of mass m and length L is taken aside and released from rest from the angular position θ as shown. If the mass takes time t to reach the lowest point. Find the magnitude of impulse of tension (in the string) on mass m from time t=0 to t.
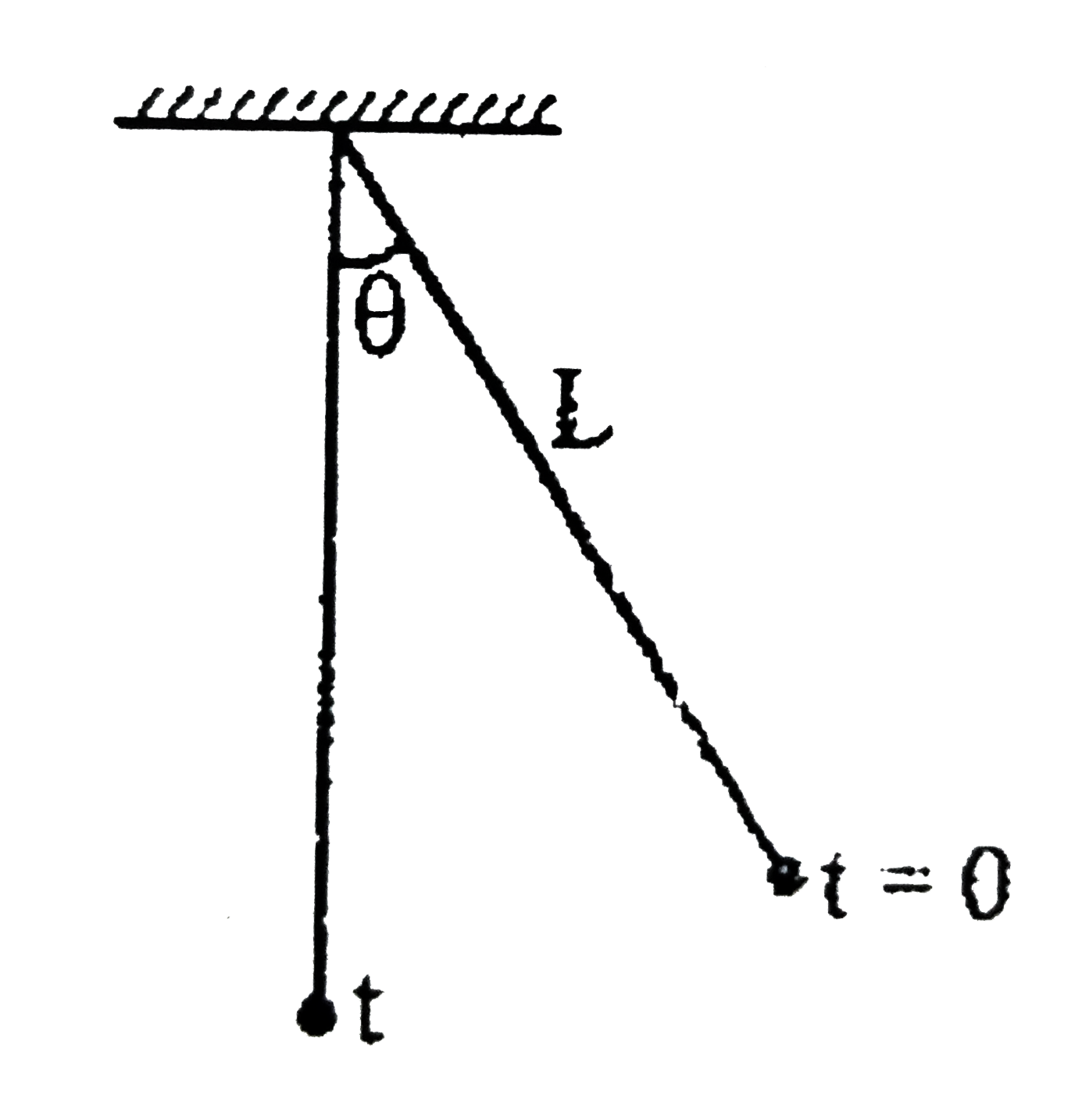
View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View SolutionA particle of mass m attached with a massless spring natural length l and stiffness k is released from rest from the horizontal position of the relaxed spring. When the particle passes through its lowest point, the maximum length of the spring becomes 2l. Find the:
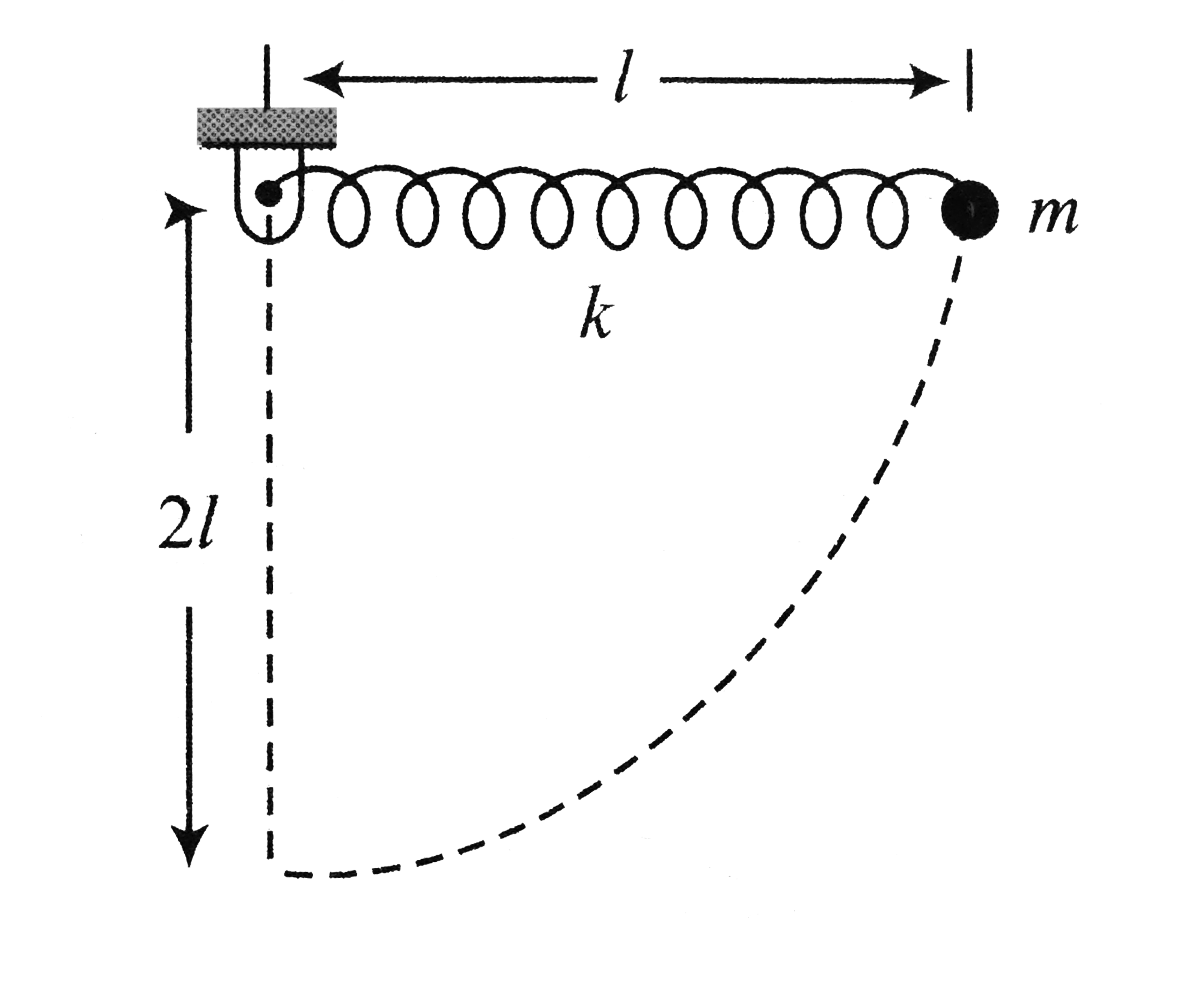
a. speed of the particle at its lowest point.
b. acceleration of the particle at its lowest position.
View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View SolutionThe length of a simple pendulum of 0.4 m. The bob of the pendulum is drawn aside till the string is horizontal, it is then released from this horizontal position, What will be its velocity when it reached the lowest point in its swing ? (g=9.8m/s2)
[Hint : Loss in potential energy = gain in kinetic energy]
View Solution
