A rigid triangular frame ABC of mass m is hanging from a rigid horizontal rod PQ. The frame is constrained to move along horizontal without friction. A bead of mass m is released from B that moves along BC. Displacement of frame when bead reaches C is
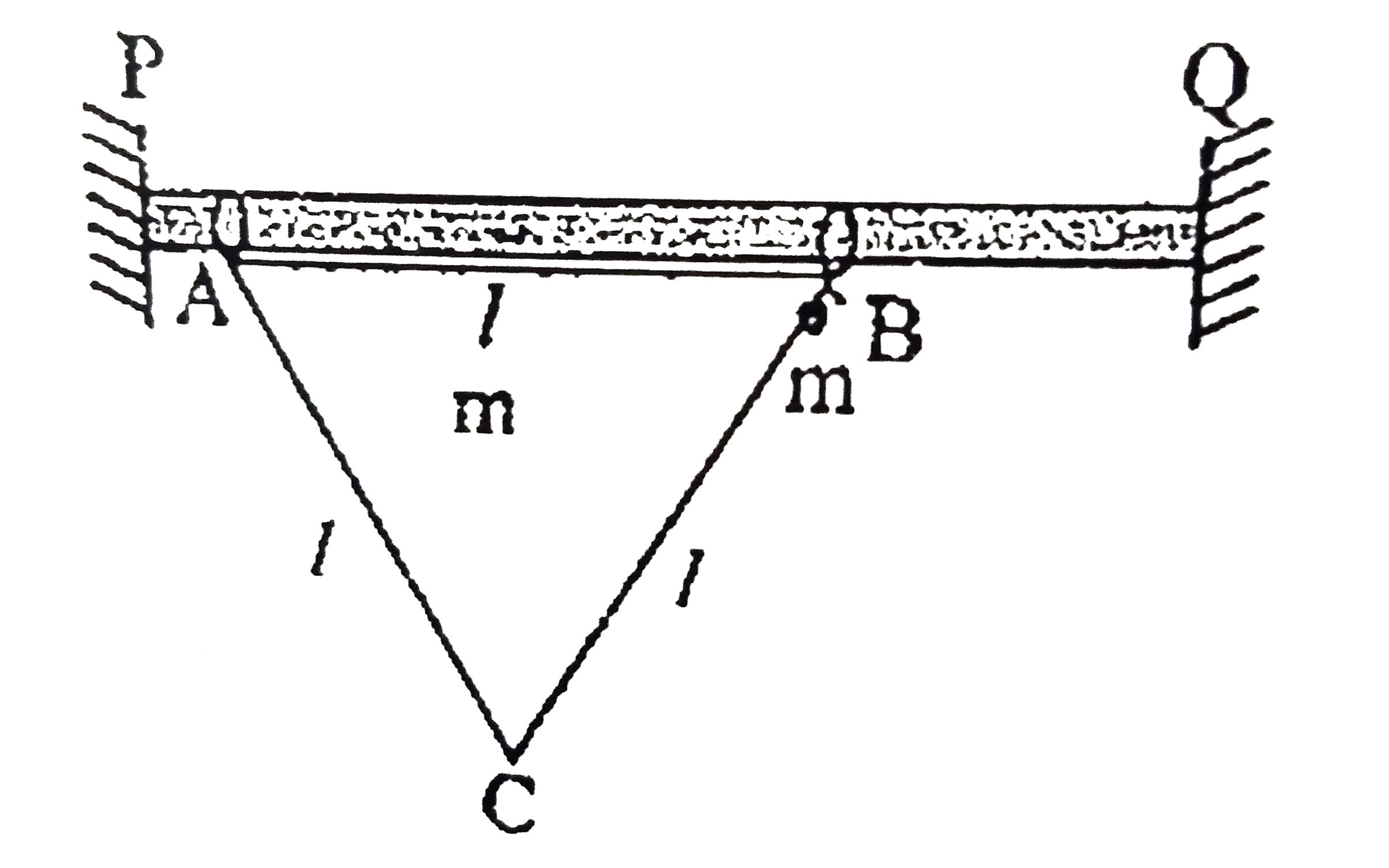
l2
l4
l4
3l√2
Step by step video, text & image solution for A rigid triangular frame ABC of mass m is hanging from a rigid horizontal rod PQ. The frame is constrained to move along horizontal without friction. A bead of mass m is released from B that moves along BC. Displacement of frame when bead reaches C is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A heavy mass m slides down a triangular prism of mass M . The prism lies on a horizontal surface and can move along it without friction . What will be the direction of motion of m if the inclination of the hypotenuse of the prism is α with the horizontal ?
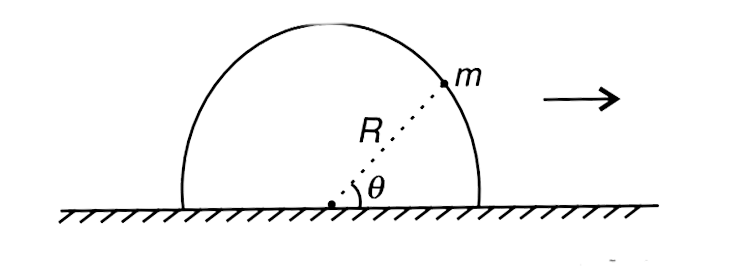
View SolutionA semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration.
View Solution
Knowledge Check
A horizontal force F is applied on a riing of mass m1 constrained to move on a horizontal smooth wire the hanging mass m2 is constant angle with
 AForce on m1 by wire is less than (m1+m2)gBNet force on m2 is m2Fm1+m2CTension in rod is m2gsecθDF=(m1+m2)gtanθ
AForce on m1 by wire is less than (m1+m2)gBNet force on m2 is m2Fm1+m2CTension in rod is m2gsecθDF=(m1+m2)gtanθA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :
 Ag2B(√3g)(2)Cg√2Dg
Ag2B(√3g)(2)Cg√2DgA man of mass m is standing on a stationary flat car of mass M. The car can move without friction along horizontal rails. The man starts walking with velocity v relative to the car. Work done by him
A(a) is greater than 12mv2 if he walks along rails.B(b) is less than 12mv2 is he walks along rails.C(c) is equal to 12mv2 is he walks normal to rails.D(d) can never be less than 12mv2
ABC is a triangular framwork of three uniform rods each of mass m and length 2l. It is free to rotate in its own plane about a smooth horizontal axis through A which is perpendicular to ABC. If it is released from rest when AB is horizontal and C is above AB. Find the maximum velocity of C in the subsequent motion.
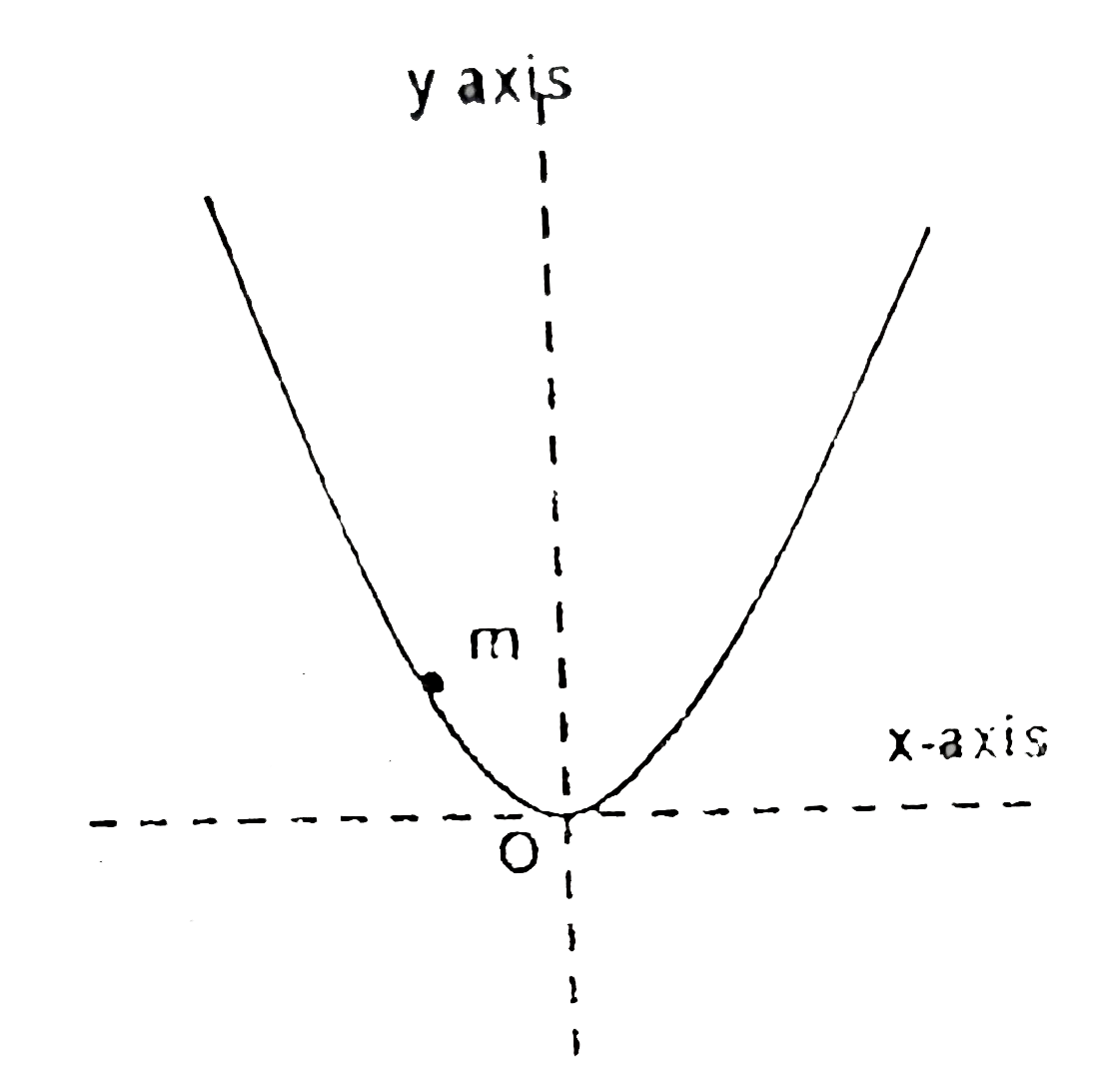
View SolutionA point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :
View SolutionThree massless rods are fixed to form a right angled triangular frame such that AB=BC=1 . Two identical small objects of mass m are fixed at A and C . The frame is hinged about B such that the frame can rotate in vertical plane about an horizontal axis without friction. Initially AB is vertical and BC is horizontal and the system is released from rest.
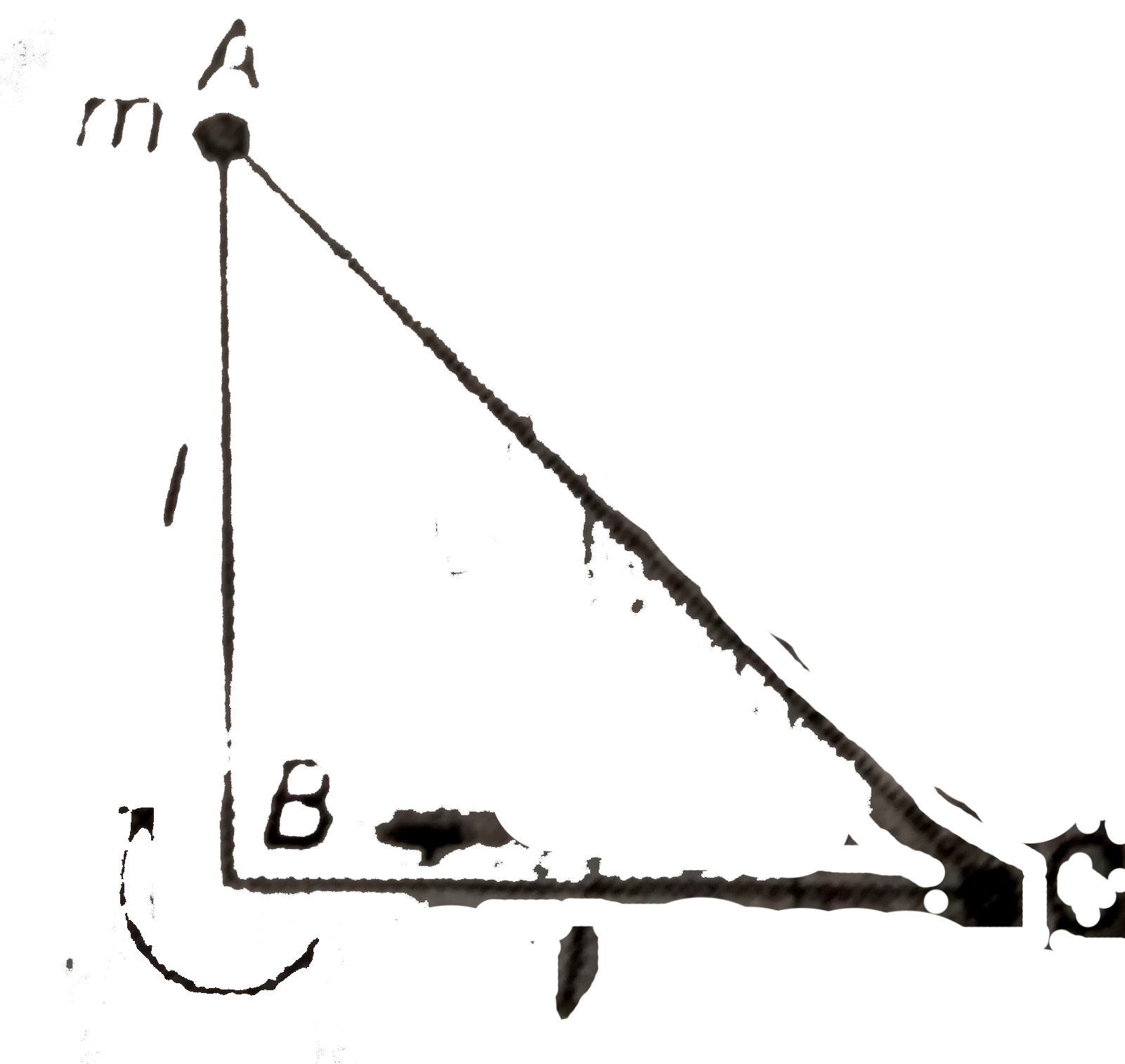
The magnitude of acceleration of mass A when the rod AC becomes horizontal is
View SolutionThree massless rods are fixed to form a right angled triangular frame such that AB=BC=1 . Two identical small objects of mass m are fixed at A and C . The frame is hinged about B such that the frame can rotate in vertical plane about an horizontal axis without friction. Initially AB is vertical and BC is horizontal and the system is released from rest.
Tension in the rod AC when it (rod AC) becomes horizontal is
View SolutionA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
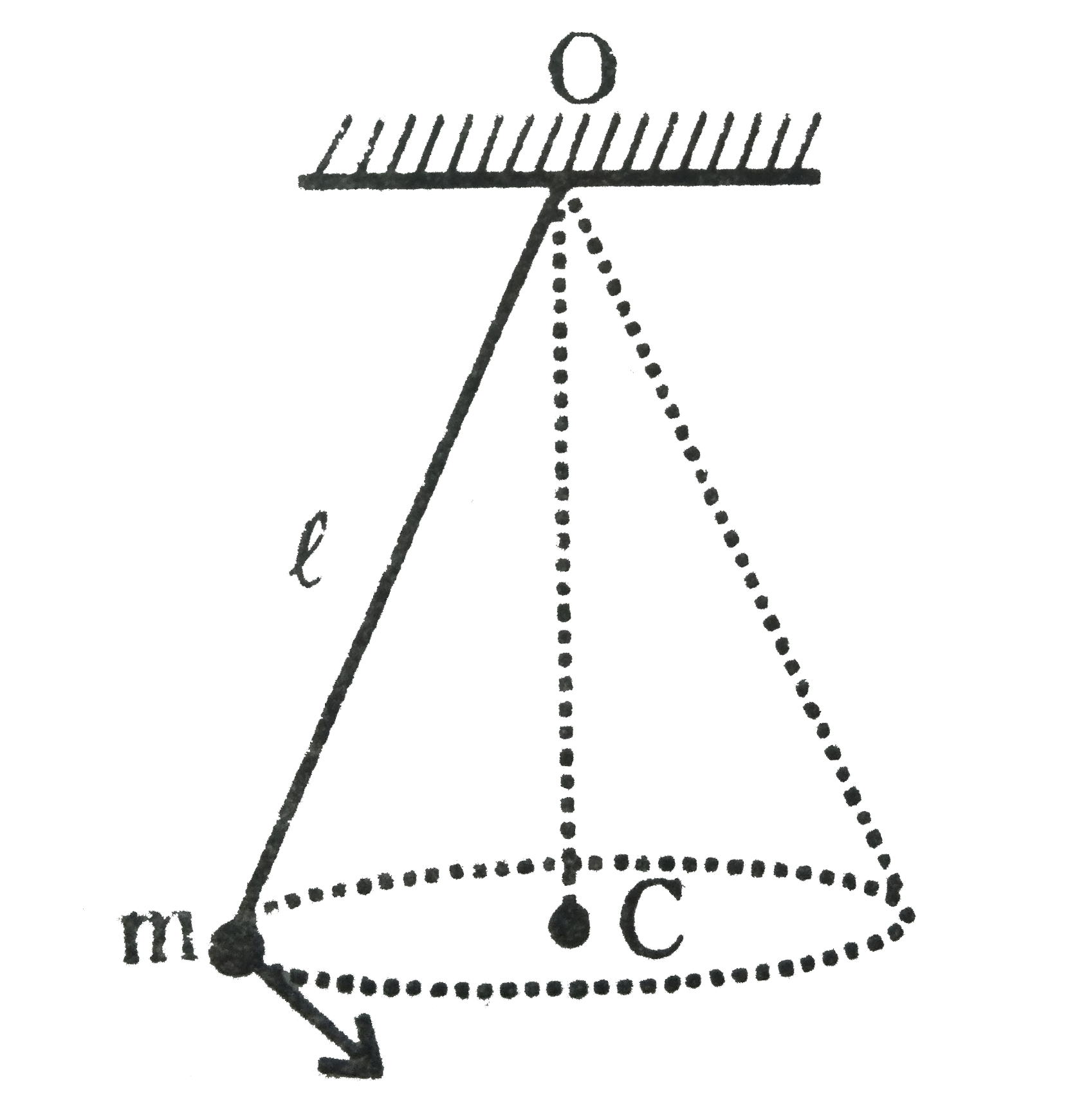 .
.
View Solution
