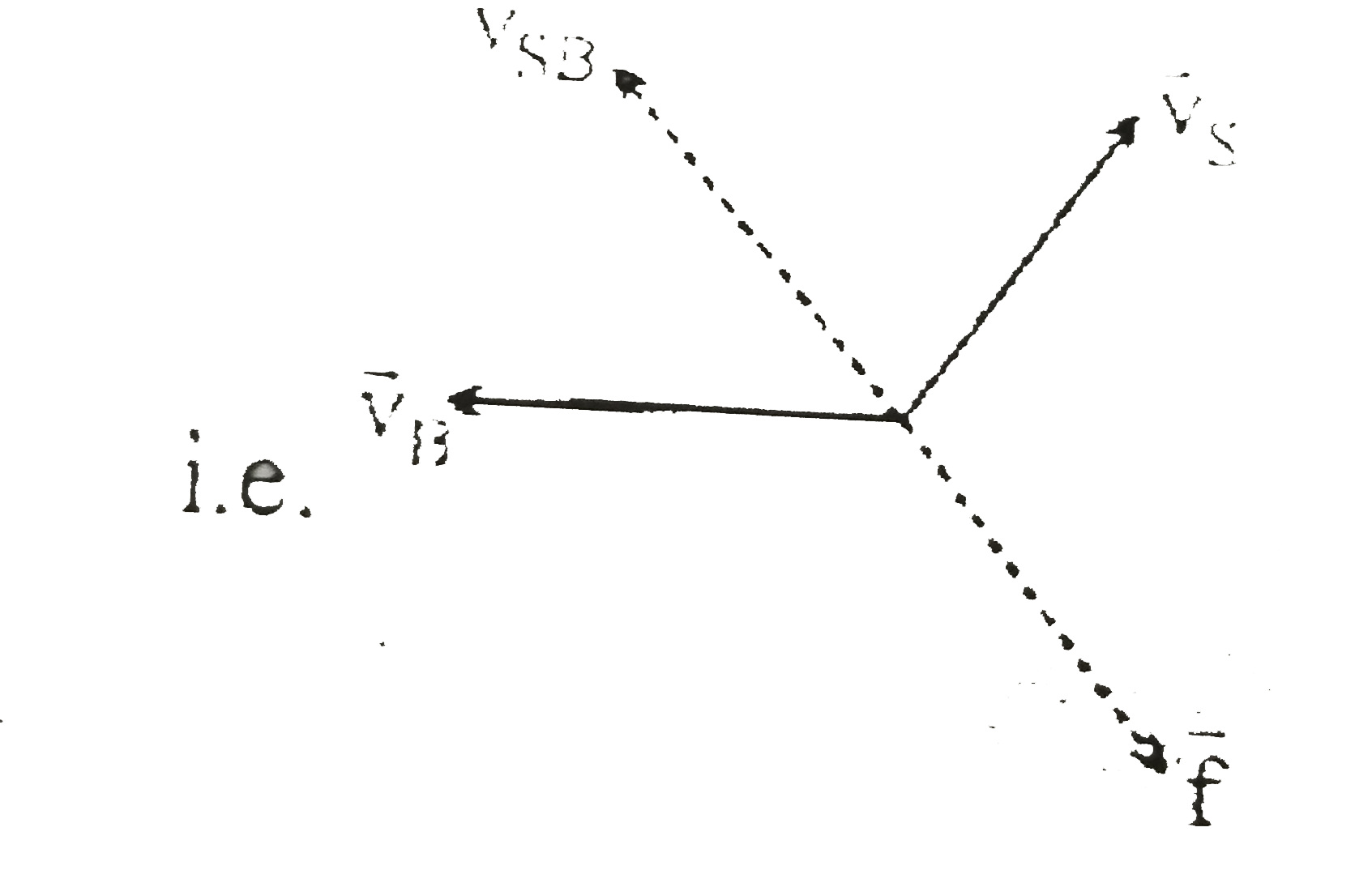
A girl is standing on ground near a horizontally moving conveyor belt. She throws her suitcase horizontally, such that the initial velocity of suitcase relative to stationary girl is along dotted line shown in top wiew of converyor belt.

Which of the follwing arrows represents the direction of friction

A
B
C
D
→vSB=→vS−→vS=→vS+(−→vB)
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A girl is standing on ground near a horizontally moving conveyor belt. She throws her suitcase horizontally, such that the initial velocity of suitcase relative to stationary girl is along dotted line shown in top wiew of converyor belt.

Which of the follwing arrows represents the direction of friction
 View Solution
View SolutionA block lying on a long horizontal conveyer belt moving at a constant velocity receives a velocity v0=5m/s relative to the ground in the direction opposite to the direction of motion of the conveyer. After t=4s, the velocity of the block becomes equal to the velocity of the belt. The coefficient of friction between the block and the belt is μ=0.2. Determine the velocity v of the conveyer belt.
View Solution
Knowledge Check
- Question 1 - Select One or More
A man of mass m is standing on a stationary flat car of mass M. The car can move without friction along horizontal rails. The man starts walking with velocity v relative to the car. Work done by him
A(a) is greater than 12mv2 if he walks along rails.B(b) is less than 12mv2 is he walks along rails.C(c) is equal to 12mv2 is he walks normal to rails.D(d) can never be less than 12mv2 - Question 2 - Select One
In one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QThe graph shows the psition of a hard ball with respect to time .The hard ball hits and rebounds on the hard surface .Ehich of the following graph represent the correct variation with repect to time?
 A
A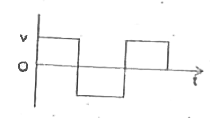 B
B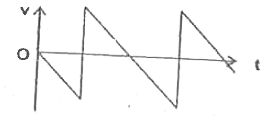 C
C Dnone of these
Dnone of these - Question 3 - Select One
A girl of mass M stands on the rim of a frictionless merry-go-round of radius R and rotational inertia I that is not moving. She throws a rock of mass m horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the rock. relative to the ground, is v. After, the linear speed of the girl is.
 .AmvR2I+MR2B(m+M)vR2I+MR2CmvR2I+(M+m)R2DmvR2I+(M−m)R2
.AmvR2I+MR2B(m+M)vR2I+MR2CmvR2I+(M+m)R2DmvR2I+(M−m)R2
A ball rests upon a flat piece of paper on a table top. The paper is pulled horizontally but quickly towards right as shwon. Relative to its initial position with respect to the table, the ball

(i) remains stationary if there is no friction between the paper and the bell.
(ii) moves to the left and starts rolling backwards, i.e. to the left if there is a friction between the paper and the ball.
(iii) moves forward, i.e. in the direction in which the paper is pulled.
(iv) Here, the correct statements/s/is/areView SolutionA horizontal conveyor belt moves with a constant velocity V.A small block is projected with a velocity of 6m/s on it in a direction opposite to the direction of motion of the belt The block comes to rest relative to the belt in a time 4s.μ=0.3,g=10.m/s2 Find V .
View SolutionFigure shown a man standing stationary with respect to a horizontal converyor belt that is accelerationg with 1m/s−2 . What is the net force on the man?If the coefficient of ststic friction between the man's shoes and the belt is 0.2 upto what maximum acceleration of the belt can the man continue to be stationary relative to the belt? Mass of the man=65kg(g=9.8m/s2)
 View Solution
View SolutionA horizontal plane supports a stationary vertical cylinder of radius R and a disc A attached to the cylinder by a horizontal thread AB of length l0 (figure, to view). An initial velocity v0
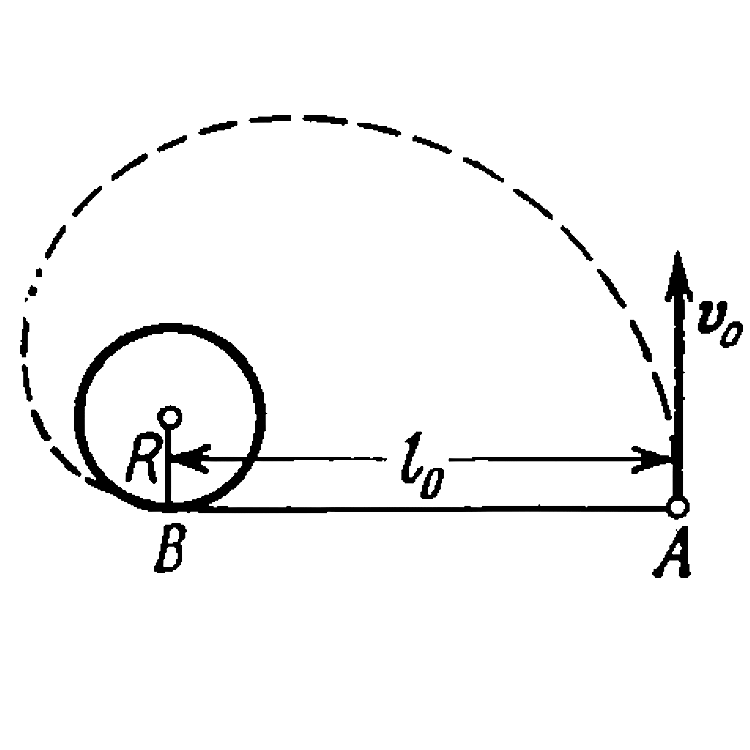
is imparted to the disc as shown in the figure. How long will it move along the plane until it strikes against the cylinder? The friction is assumed to be absent.View SolutionA and B are two identical blocks of same mass 2 m and same physical dimensions as shown in figure −4.158 A is placed over the block B which is attached to one end of the spring of natural length l and spring contant k. The other end of the speing is attached to a wall. The system is resting on a smooth horizontal surface with the spring in the relaxed state. A small object of mass m moving horizontally with speed v at a height d above the horizontal surface hits the block B along the line of therir cntre of mass in a perfectly elastic collision. There is no friction between A and B.
Find the minimum value of v (sayvo)such that the block A will topple over block B.
What is the energy stored in the spring when the blocks A and B returns to their initial position as before collision
 View Solution
View Solution

