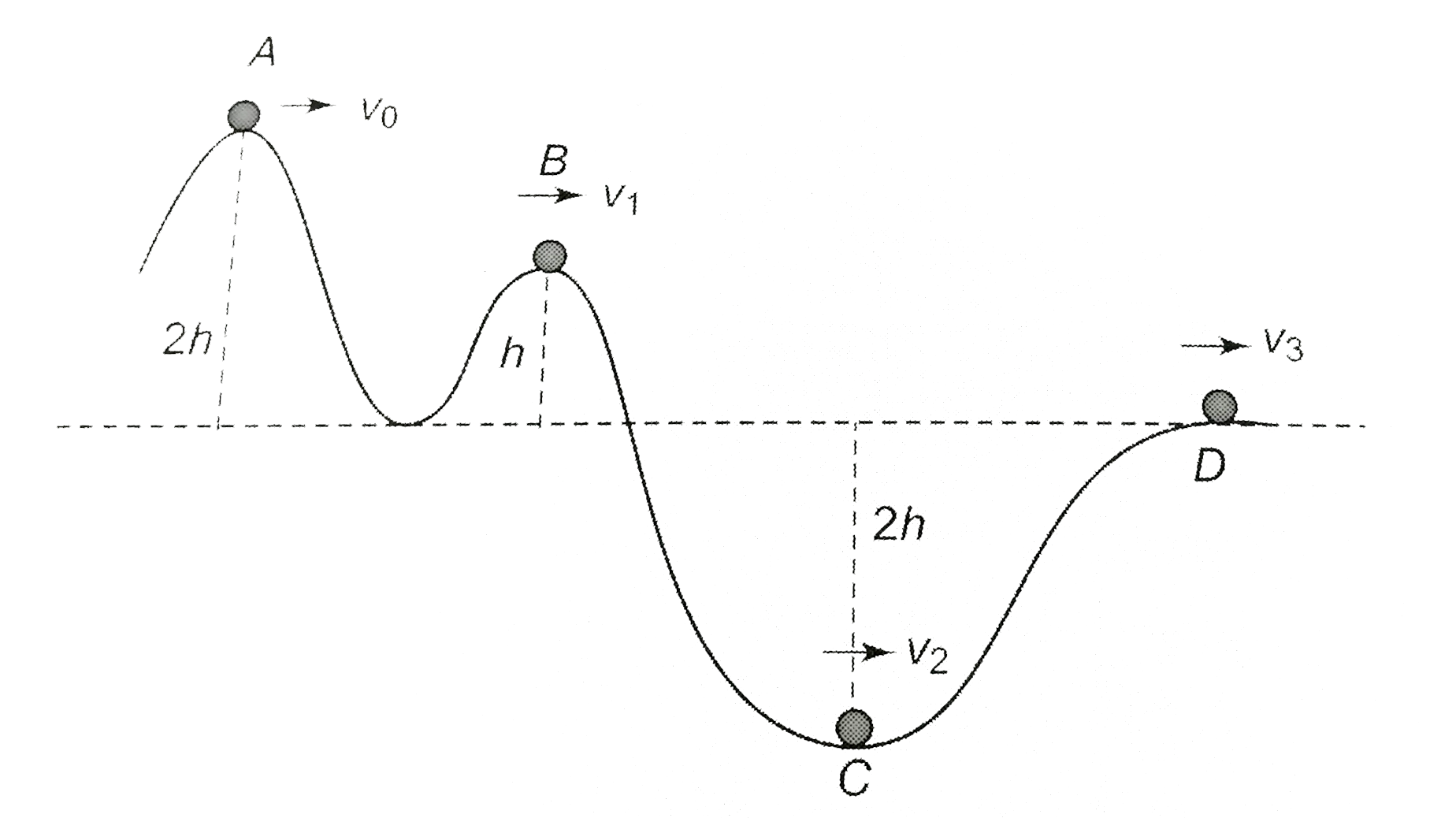
Four rods of equal length L are joined by four pins A,B,C & D as shown in the figure. Rods are free to rotated about pins. Pin A is given velocity v0 and pin C is given 3v0 as shown
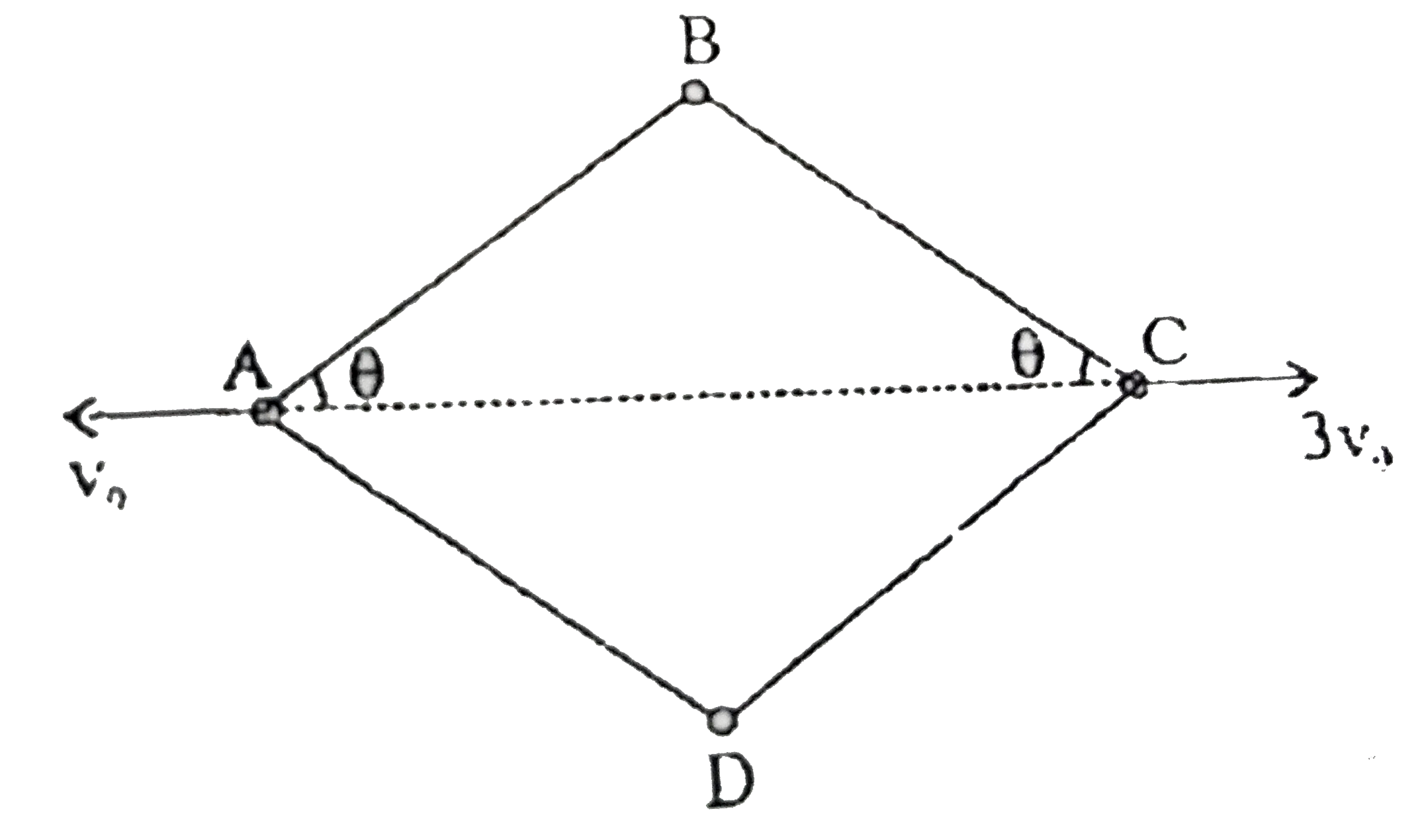
The speed of pin B with respect to pin A is
2v0cosθ
2v0sinθ
2v0
None of these
vsinθ+2v0cosθ=4v0cosθ
⇒v=2v0cotθ
∴vB=2v0cosecθ
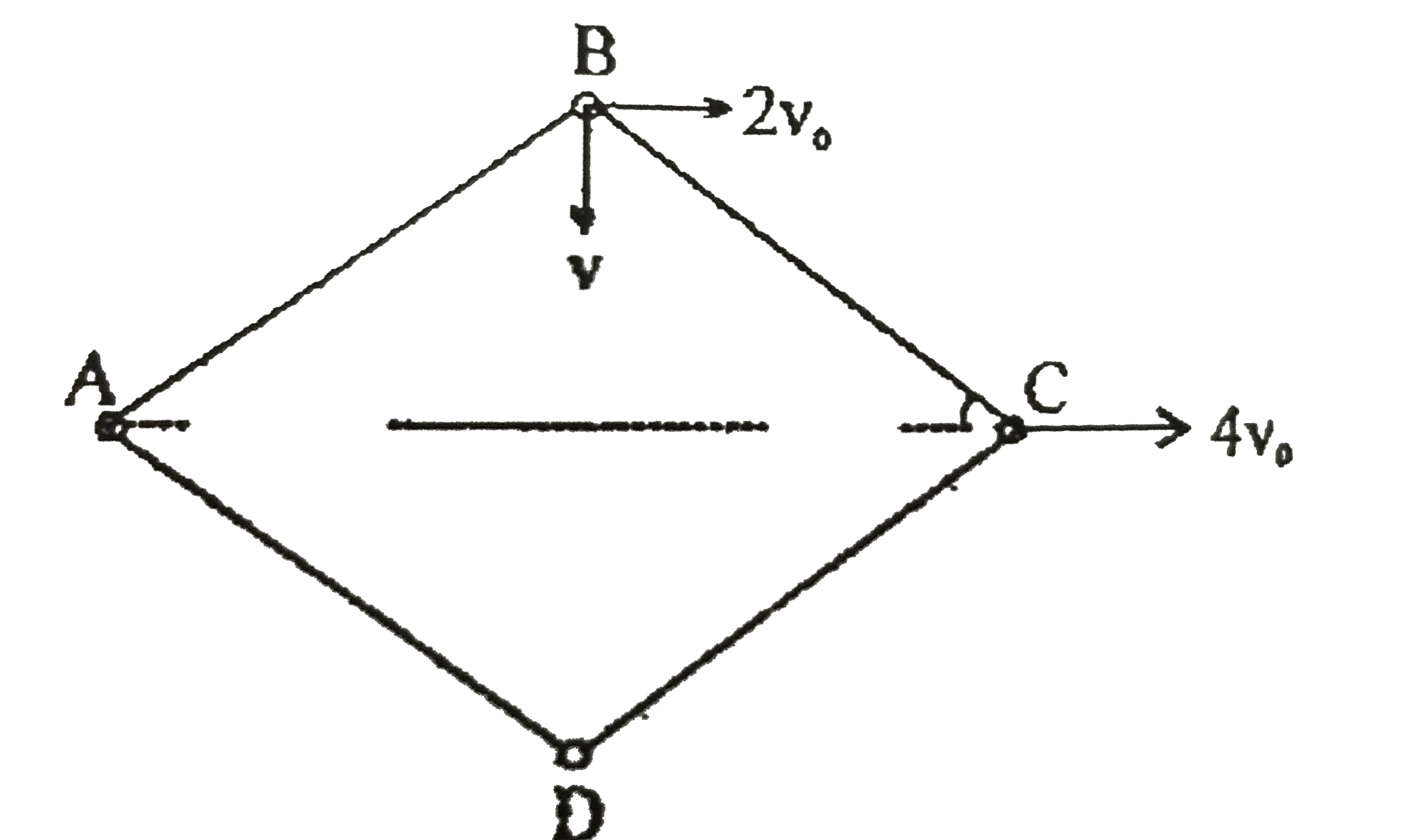
ω=2v0sinθ+vcosθL=2v0Lsinθ
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Knowledge Check
Four rods of equal length L are joined by four pins A,B,C & D as shown in the figure. Rods are free to rotated about pins. Pin A is given velocity v0 and pin C is given 3v0 as shown
The angular velocity of rod BC isA2v0LB2v0LsinθC2v0LsinθD2v0LcosθTwo identical rods are joined at one of their ends by a pin. Joint is smooth and rods are free to rotate about the joint. Rods are released in vertical plane on a smooth surface as shown in the figure. The displacement of the joint from its initial position to the final position is (i.e. when the rods lie straight on the groun )
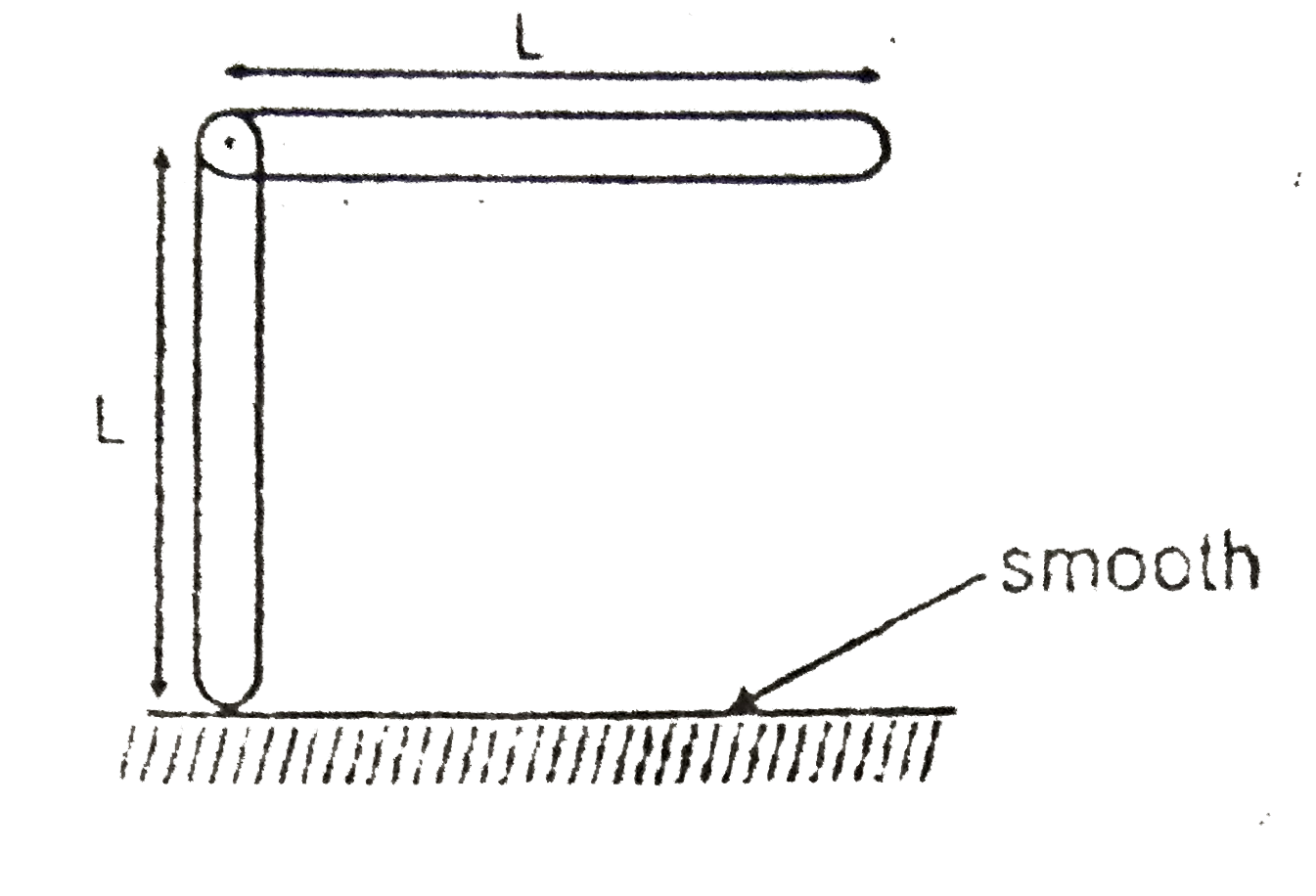AL4B√174C√15L2Dnone of these
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:A12mVLcosθB13mVLsinθCmVLsincosθDzero
Two identical rods are joined at one of their ends by a pin. Joint is smooth and rods are free to rotate about the joint. Rods are released in vertical plane on a smooth surface as shown in the figure. The displacement of the joint from its initial position to the final position is (i.e. when the rods lie straight on the groun )
View SolutionA smooth disc of mass M and radius L√3 is placed at rest horizontally on a smooth horizontal surface. A massless pin is fixed at point P at a distance L/2 from centre O of the disc as shown in the figure. Now a thin uniform rod of mass M and length L is placed horizontally on the surface of the disc parallel to the line OP such that its mid point and centre O of the disc just coincide as shown in figure. Now rod has given angular velocity ω0=24rad/sec in counter clockwise direction as shown. As a result, the end of the rod strikes the pin P and stricks to it rigidly. Calculate the angular velocity of disc just after collision.
View SolutionA smooth disc of mass M and radius L√3 is placed at rest horizontally on a smooth horizontal surface. A massless pin is fixed at point P at a distance L/2 from centre O of the disc as shown in the figure. Now a thin uniform rod of mass M and length L is placed horizontally on the surface of the disc parallel to the line OP such that its mid point and centre O of the disc just coincide as shown in figure. Now rod has given angular velocity ω0=24rad/sec in counter clockwies direction as shown. As a result, the end of the rod strikes the pin P and stricks to it rigidly. Calculate the angular velocity of disc just after collision.
View Solution-
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution -
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution