ABCD is a quadrilateral in which and∠DAB =∠CBA(see Fig. 7.17). Prove that
(i) ΔABD≅ΔBAC
(ii) BD = AC
(iii) ∠ABD =∠BAC

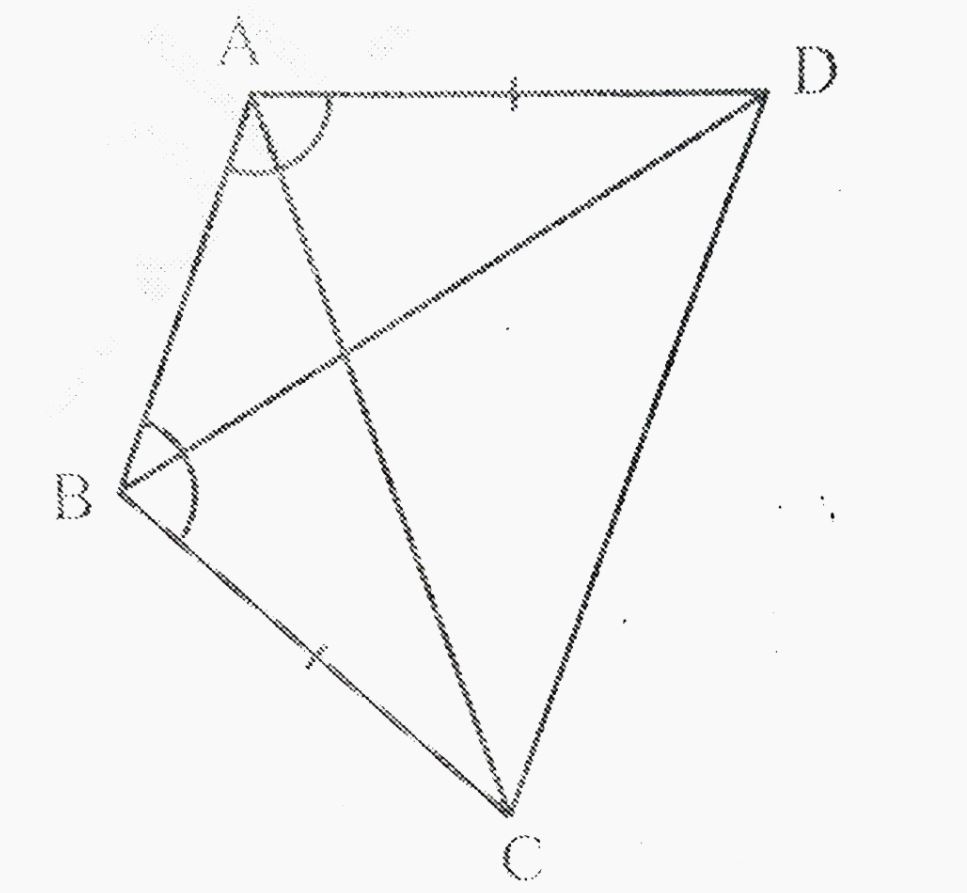
(i) In △ABD and △BAC,
AD=BC (Given)
∠DAB=∠CBA(Given)
AB=BA (Common)
∴ △ABD≅△BAC (By SAS congruence rule)
(ii) Since △ABD≅△BAC,
∴ BD=AC (By CPCT)
(iii) Since △ABD≅△BAC,
∠ABD=∠BAC (By CPCT)
Topper's Solved these Questions
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.8
10 Videos
Similar Questions
Knowledge Check
If ABCD is a cyclic quadrilateral with ∠A=50∘,∠B=80∘, then Cand∠D are
A100∘,130∘B115∘,115∘C110∘,120∘D130∘,100∘
ABCD is a parallelogram in which ∠A=70∘ Compute ∠B, ∠C and ∠D
View SolutionABCD is a parallelogram in which ∠A=70∘. Compute ∠B, ∠C and ∠D.
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD

View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
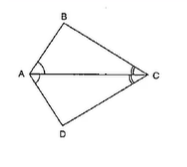
View Solution


