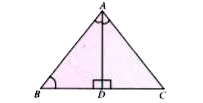
In ⋀ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
∠ABDand∠ACD
∠BAD=∠CAD
AD=AD
∠ADB=∠ADC=900
∠ABD≅∠ACD(ASA)
AB=AC
BD=CD
∠ABD=∠ACD
∠ABC is a Isosceles.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.46videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.18videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.28videos
TRIANGLES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.810videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
In a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
A10B12C14D√221
AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
 View Solution
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
 View Solution
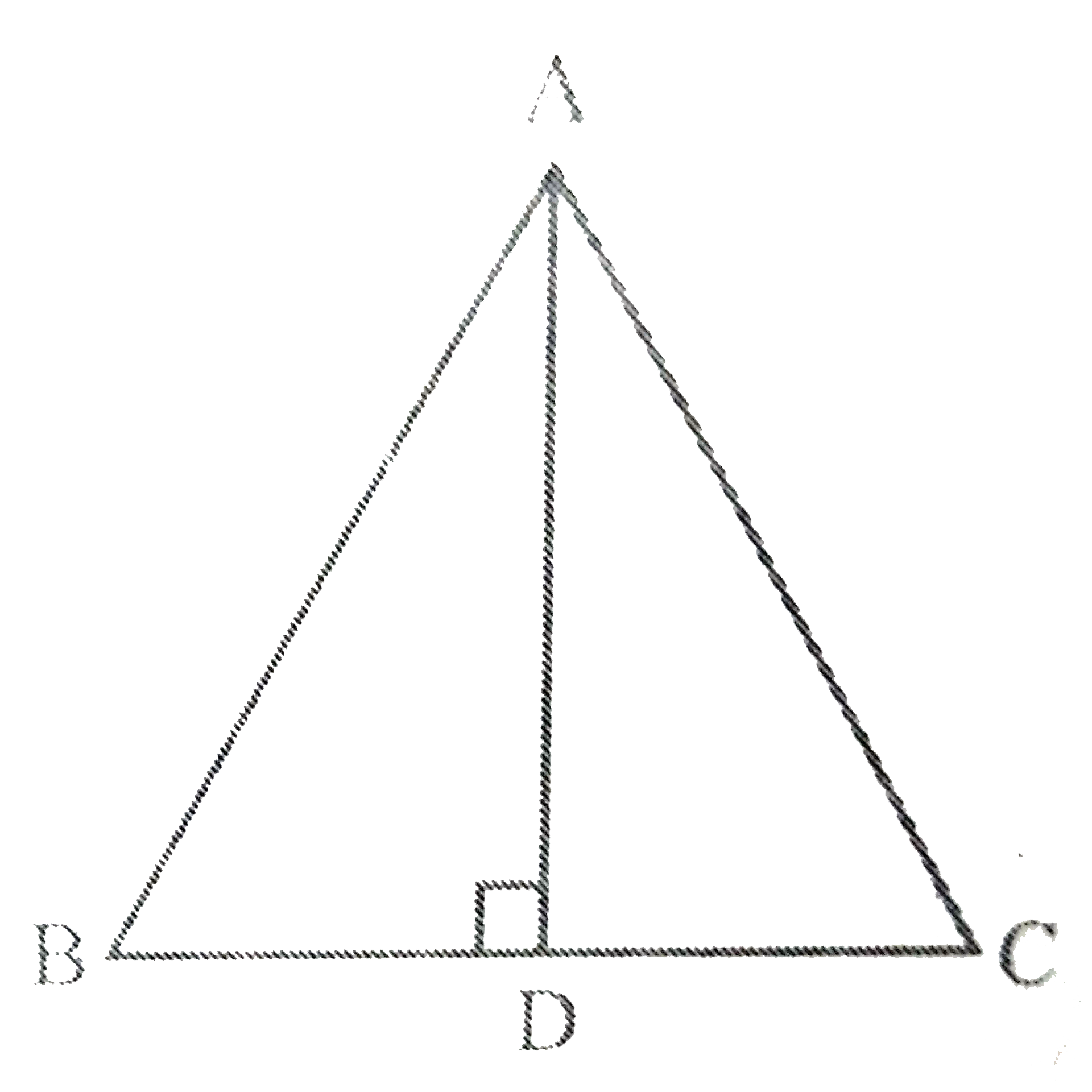
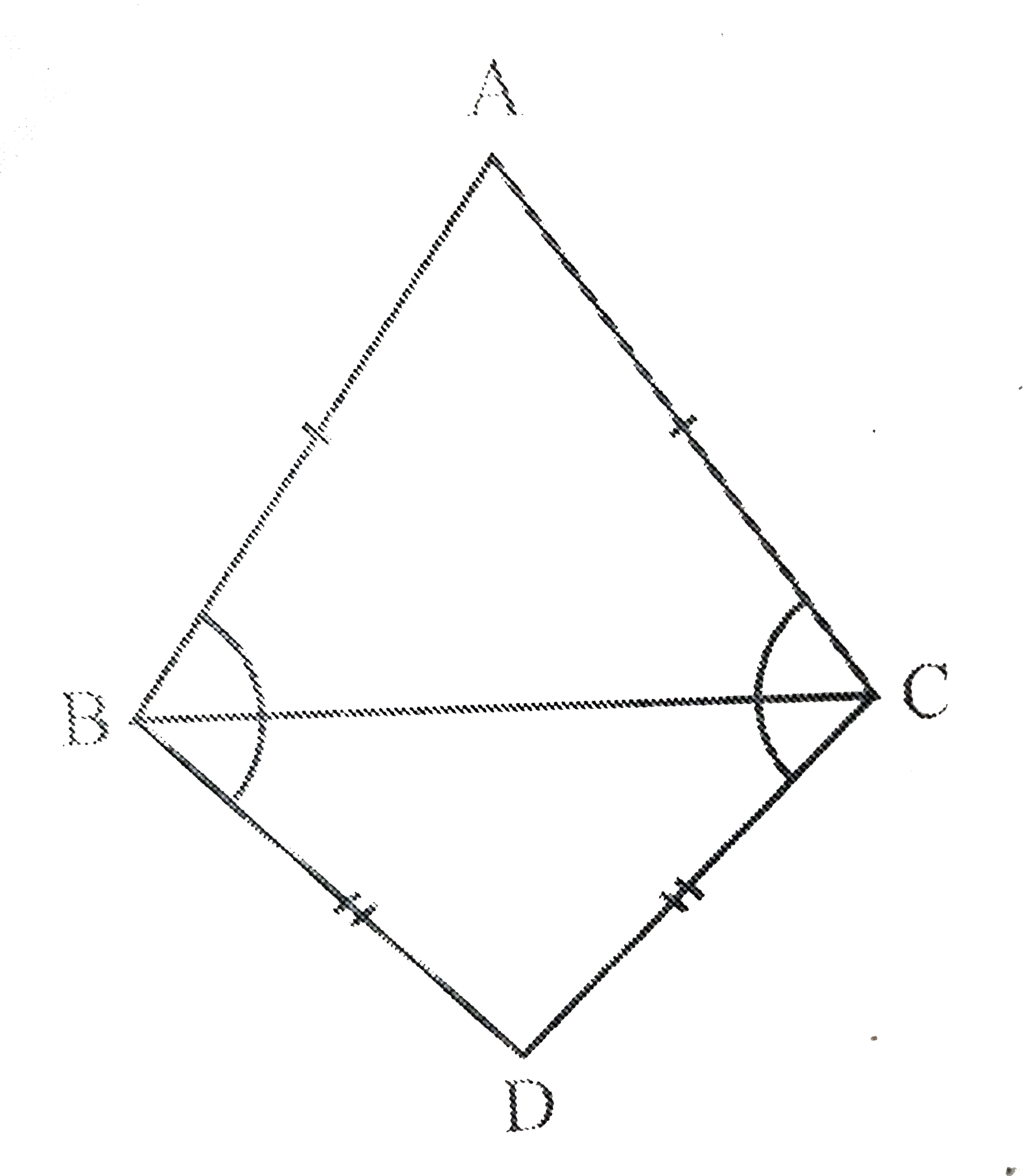
View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD
 View Solution
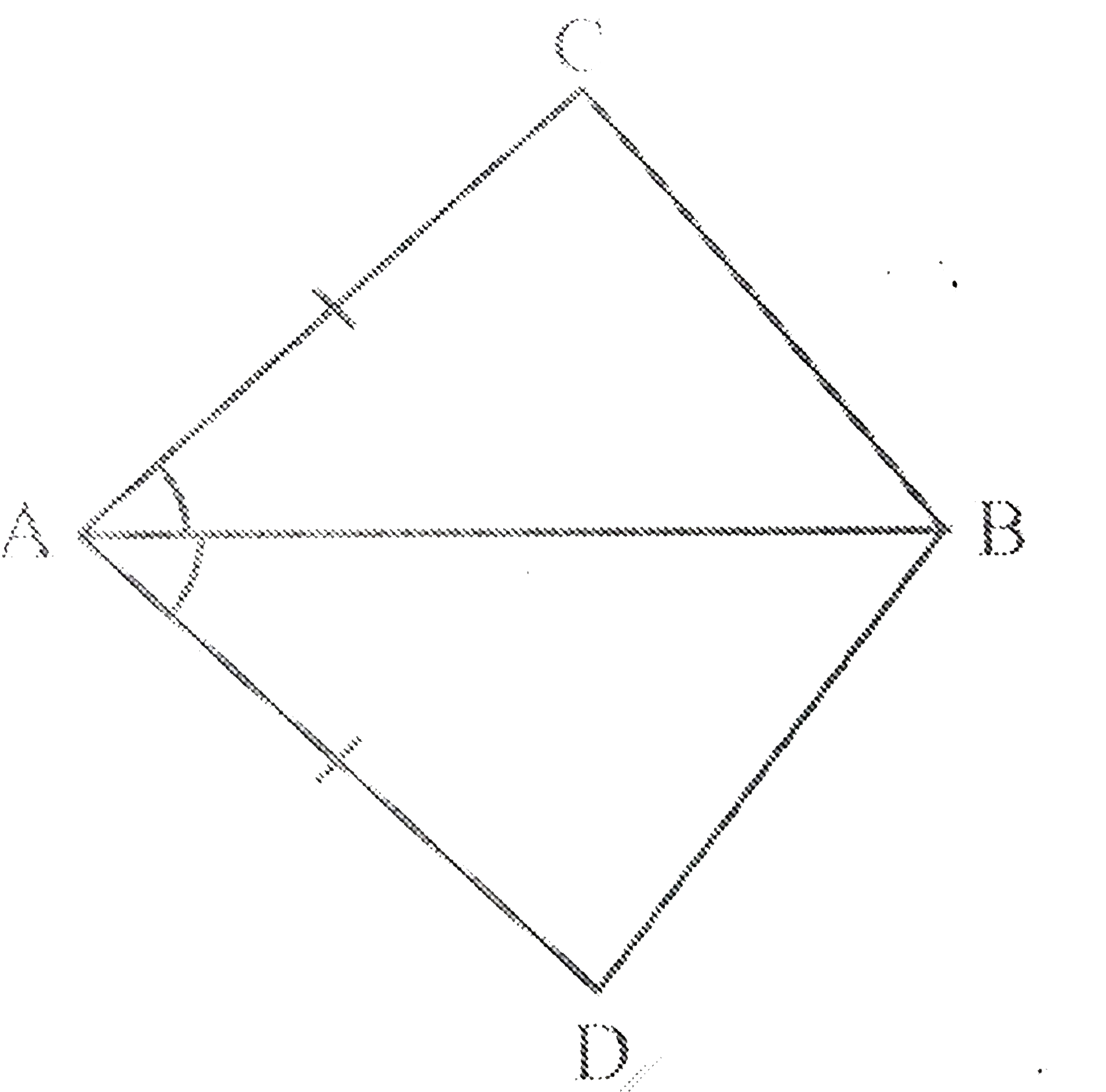
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
 View Solution
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
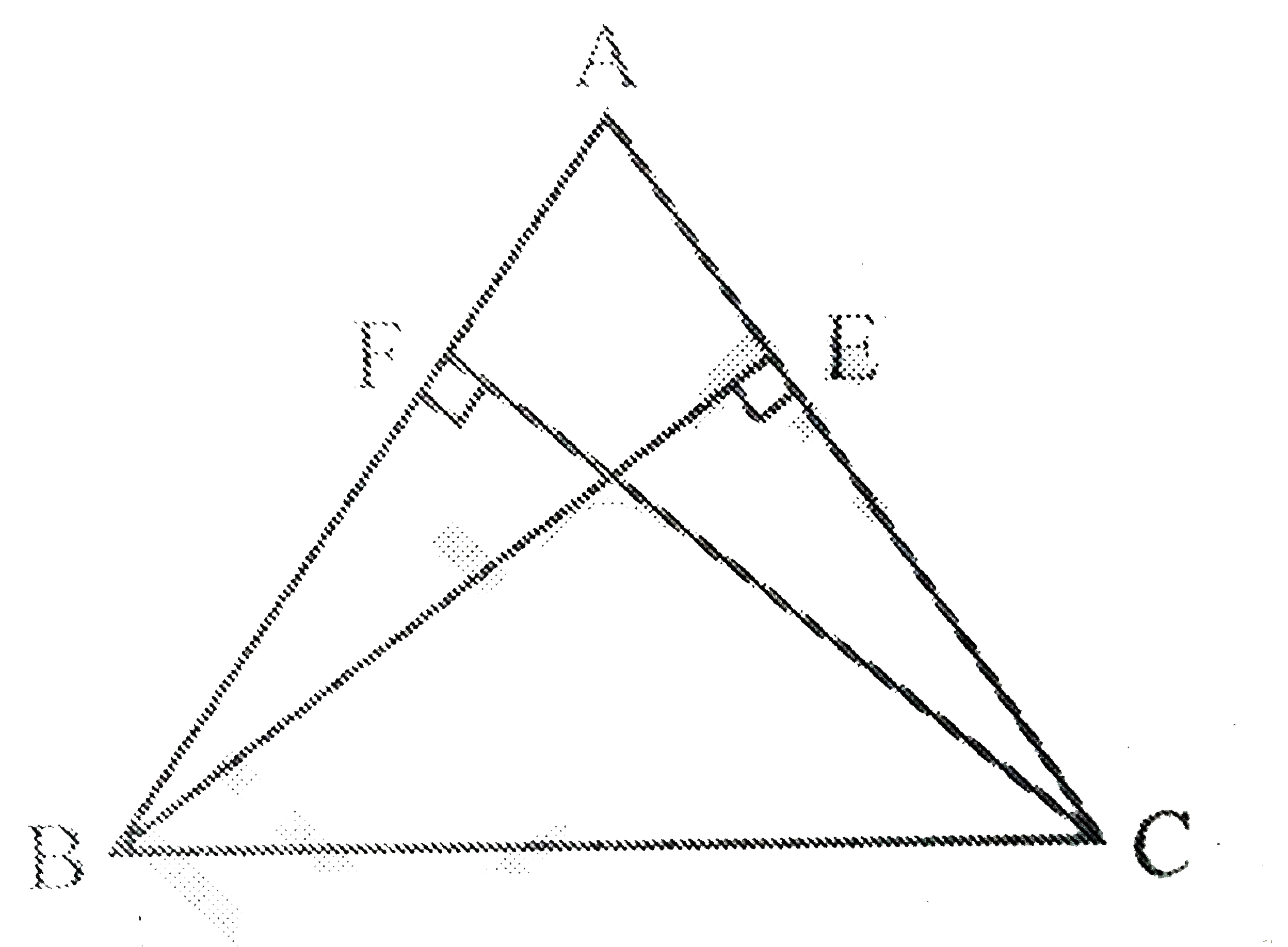 View Solution
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
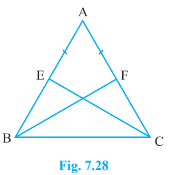 View Solution
View Solution