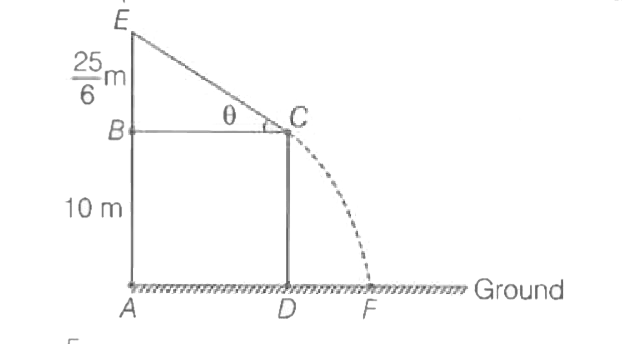
A rough inclined plane BCE of height (256)m is kept on a rectangular wooden black ABCD of height 10 m , as shown in the figure. A small block is allowed to slide down from the top E of the inclined plane. The coefficient of kinetic friction between the block and the inclined plane is 18 and the angle of inclination of the inclined plane is sin−1(0.6). IF the small block finally reaches the ground at a point F, then DF will (Acceleration due to gravity, g=10ms−2)
 Solution in Telugu
Solution in Telugu
53m
103m
133m
203m
According to question, a small block is slide down from top E of inclined plane as shown in figure,
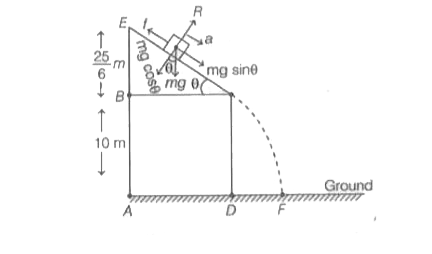
Force equation of a block
⇒mgsinθ−f−ma
∵ friction force applied one block f=μkR
or f=μkR(mgcosθ) ( From figure)
Where, μk = coefficient of kinetic friction
from Eq (i) we get
⇒mgsinθ−μkmgcosθ=ma
⇒a=10sinθ−1/8×10cosθ.....(ii)(∵μk=18,given)
∵ Given angle of the inclined plane, θ=sin−1(0,6)
or sinθ=0.6
∵cosθ=√1−sin2θ=√1−(0.6)2
∴cosθ=0.8
From Eq (ii)
a=10(0.6)−18×10(0.8)ora=5ms−2
When, block reached to point C, then from third equation of the motion,
v2=u2+2as
Where v= final velocity of the block at point C u= initial velocity of block at point E
or v=√2as(∵u=0)
From ΔEBC,EC=BEsinθ⇒s=25/60.6=256×0.6
ors=12518m
Hence, v=√2×5×12518=253ms−1
From second equation of motion of the block at point C,

In y- direction
⇒h=ut+12>2
⇒10=usinθt+12>2
⇒10=253×0.6t+12×10×t2
⇒253×610t+12×10×t2=10
⇒5t+5t2=10
⇒t2+t−2=0ort=1sec
Now, again from second Eqs. of motion in x-direction
⇒DF=vcosθt+0orDF=253×0.8=203m
Topper's Solved these Questions
- AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)EXERCISE - Physics
40 Videos
- AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)EXERCISE - Physics
40 Videos
Similar Questions
N divisions on the main scale of a vernier calipers coincide with (N +1) division of the vernier scale. If each division of main scale is a units, then the least count of the calipers is :
View SolutionA monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
View Solution(a) A block slides down an incline of angle 45^(@) with an acceleration (g)/(2 sqrt(2)) . Find the friction coefficient. (b) A block slides down at 45^(@) inclined plane in twice the time it takes to slide down a smooth 45^(@) incline. What is friction co-efficient between the block and the incline? ( c) A block slides down on a rough inclined plane of inclination 30^(@) with constant velocity. If this block is projected up the plane with a velocity of 10 m//s , then at what distance along the inclined plane , the block will come to rest? (d) A body is launched up on a rough inclined plane of inclination theta . If time of ascent is half of time of descent, find the friction coefficient.
View SolutionA block is released from the top of an inclined plane of inclination theta . Its velocity at the bottom of plane is v . If it slides down a rough inclined plane of the same inclination , its velocity at bottom is v//2 . The coefficient of friction is
View SolutionA block sliding down on a rough 45^(@) inclined planes has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the the block and the inclined plane is
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA body freely released from A slides down a smooth inclined plane 'AB' and then a rough incline plane 'BC' such that BC = N (AB). If the block comes to rest at C, then coefficient of kinetic friction between the block and inclined plane is?
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination theta and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionA block sliding down on a rough 45∘ inclined plane has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the block and the inclined plane is
View SolutionA block sliding down a rough 45° inclined plane has half the velocity it would have had, the inclined plane been smooth. The coefficient of sliding friction between block and the inclined plane is
View SolutionA block sliding down a rough 45^(@) inclined plane has half the velocity it would have had, the inclined plane been smooth. The coefficient of sliding friction between block and the inclined plane is
View SolutionA block sliding down a rough 45° inclined plane has half the velocity it would have had, the inclined plane been smooth. The coefficient of sliding friction between block and the inclined plane is
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA block sliding down a rough 45^(@) inclined plane has half the velocity it would have had, the inclined plane been smooth. The coefficient of sliding friction between block and the inclined plane is
View Solution
