Question

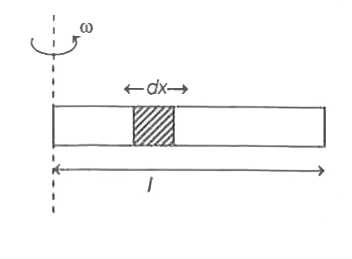
A uniform rod of length l and density ${\displaystyle \rho }$ is revolving about a vertical axis passing through its one end. If ${\displaystyle \omega }$ is the angular velocity of the rod then the centrifugal force per unit area of the rod is

Options

A. `(rhoomega^(2//2))/(4)`
B. `(rhoomega^(2//2))/(12)`
C. `(rhoomega^(2//2))/(2)`
D. `(rhoomega^(2//2))/(8)`

Answer

C

Explanation

According to the question , a uniform rod of length l and density `rho` as shown in the figure below,
`:.` Centrifugal force per unit area of rod for small length dx is
`underset(0)overset(F) intdF = underset(0) overset(l)int (m omega^(2) dx)/(A)`
Let A is the area of rod and x is variable length of the rod then density of rod , `rho = (m)/(A*x) or m = rho A x`
`rArr F = rho (omega^(2))/(A) underset(0)overset(l)intA*x dx`
`rArr F = rho omega^(2) ((x^(2))/(2))_(0)^(1) = (rho omega^(2)l^(2))/(2)`