A particle moves in the xy - plane with velocity v = the magnitudes of tangential and normal accelerations respectively are
The correct Answer is:A
Given velocity of particle is v =
So
Magnitude of tangential acceleration is
or
Now substituting we get
Also total acceleration of particle is a
or magnitude of total acceleration is
Hence normal acceleration is
So magnitude of normal acceleration
Now with t we get
Topper's Solved these Questions
Similar Questions
A particle moves in the x-y plane with the velocity ¯v=aˆi−btˆj. At the instant t=a√3/b the magnitude of tangential, normal and total acceleration are _&_.
View SolutionA particle moves in the x-y plane with the velocity ¯v=aˆi−btˆj. At the instant t=a√3/b the magnitude of tangential, normal and total acceleration are _&_.
View Solution
Knowledge Check
A particle moves in the X-Y plane with velocity →v=αˆi+βtˆj. At t=α√3β the magnitude of tangential, normal and total accelerations respectively are
A√32β,β2andβBβ2,β2andβC√2β,√2βandβDNone of theseA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
A1/αB√αC1/√αDα
A particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
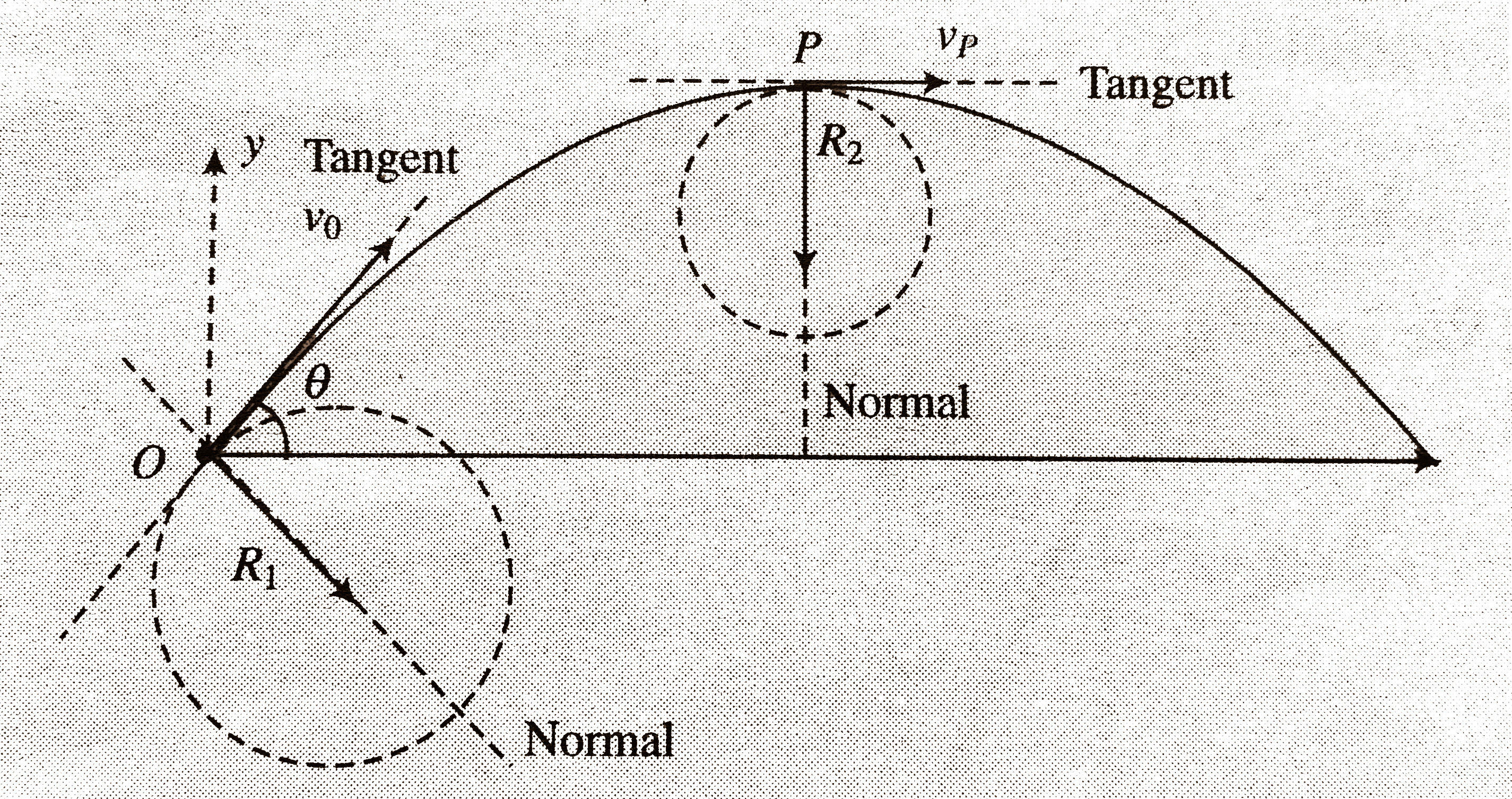 .
.
View SolutionA particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
 .
.
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v.
View SolutionA particle moves in xy plane with its position vector changing with time (t) as →r=(sint)ˆi+(cost)ˆj ( in meter)
Find the tangential acceleration of the particle as a function of time. Describe the path of the particle.
View Solution
