A body of mass m is at rest on a smooth horizontal plane. A force F = kt is applied on the body making an angle α with the horizontal. In the equation of force, t is time and k is a constant. At the instant the object loses contact with the plane, how far will it move along the plane and what will be its velocity?
As F = kt, force increases with time. Vertical component of the force = Fsinα. The body loses contact with the plane when the vertical force equals the weight of the body. i.e., Fsinα = mg . Let the time after which the body loses contact be t0.
∴ Fsinα=kt0sinα=mg
∴ t0=mgksinα
Horizontal component of the force F = Fcosα = kt cosα
Hence horizontal acceleration = ktcosαm=dvxdt
∴ dvx=ktcosαm⋅dt
Integrating , vx=kcosαmt22+A
[where A = integration constant]
As the body starts from rest, at t = 0, v = 0.
Inserting this in equation (1), A = 0.
∴ vx=kcosα2mt2
If the displacement along the plane is s, then
∴ vx=dsdt=kcosα2mt2or,ds=kcosα2mt2dt
Integrating again, s = kcosα6mt3+B
[where B = integration constant ]
As at the initial moment, the displacement is zero, i.e., at t = 0, s = 0.
From equation (3), we get B = 0.
Inserting the value of B in equation (3),
s=kcosα6mt3
Hence, displacement along the plane in time t0,
s0=kcosα6mt30=kcosα6m(mgksinα)3
or, s0=m2g3cosα6k2sin3α
and corresponding velocity, v0=kcosα2m(mgksinα)2
∴ v0=mg2cosα2ksin2α

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - SECTION RELATED QUESTION
10 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - HIGHER ORDER THINKING SKILL (HOYS) QUESTIONS
26 Videos
- NATURE OF VIBRATIONBOOK - CHHAYA PUBLICATIONCHAPTER - NATURE OF VIBRATIONEXERCISE - EXERCISE (CBSE SCANNER)
2 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - CBSE SCANNER
19 Videos
Similar Questions
At t=0, a force F = kt is applied on a block of mass m making an angle α with the horizontal . Suppose surfaces to be smooth. Find the velocity of the body at the time of breaking off the plane.

View SolutionAt t=0, a force F = kt is applied on a block of mass m making an angle α with the horizontal . Suppose surfaces to be smooth. Find the velocity of the body at the time of breaking off the plane.

View Solution
Knowledge Check
A particle is on a smooth horizontal plane. A force F is applied whose F-t graph is given. Then,
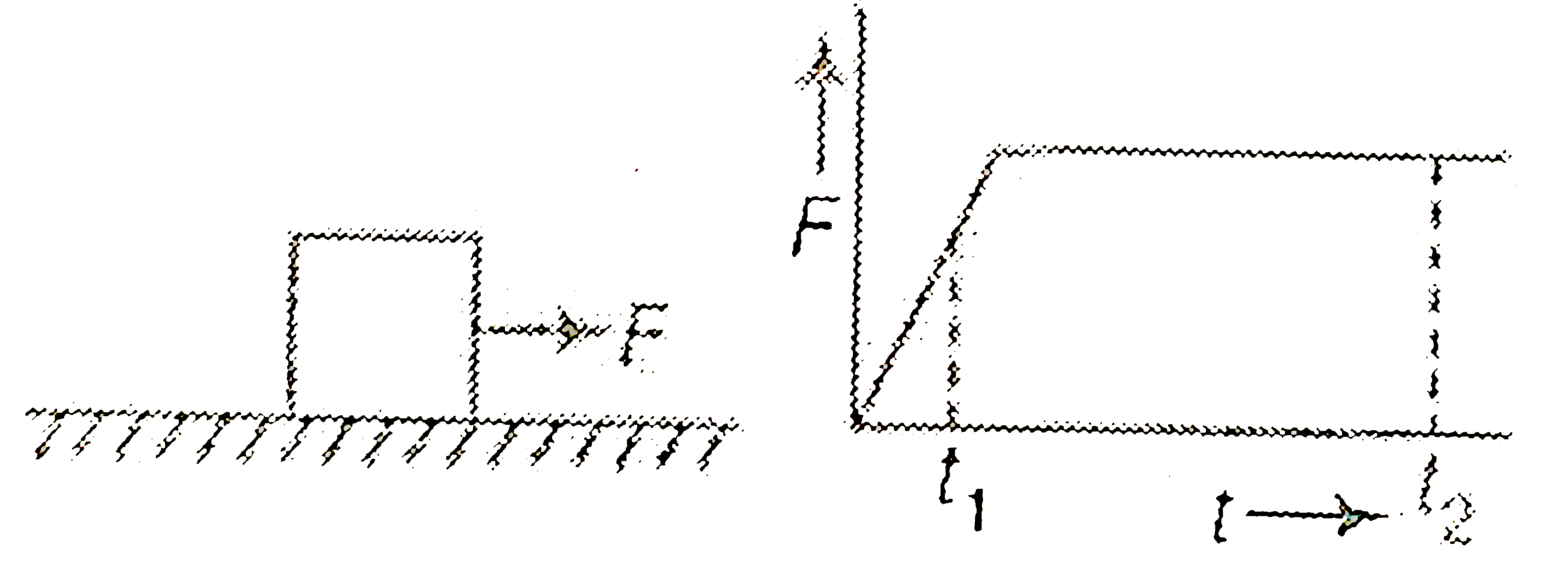 Aat t1, acceleration is constantBinitially body must be in restCat t2, acceleration is constantDboth c and d are correct
Aat t1, acceleration is constantBinitially body must be in restCat t2, acceleration is constantDboth c and d are correctA body rests on a rough horizontal plane. A force is applied to the body directed towards the plane at an angle θ with the vertical. The body can be moved along the plane
Aonly if θ is greater than the angle of frictionBonly if θ is lesser than the angle of frictionConly if θ is equal to the angle of frictionDfor all values of θA body rests a rough horizontal plane A force is applied to the body directed towards the plane at an angle θ with the vertical. The body can be moved along the plane .
Aonly if θ is greater than the angle of frictionBonly if θ is lesser than the angle of frictionConly if θ is equal to the angle of frictionDfor all values of θ
At t=0, a force F=at2 is applied to a small body of mass m at an angle α resting on a smooth horizontal plane
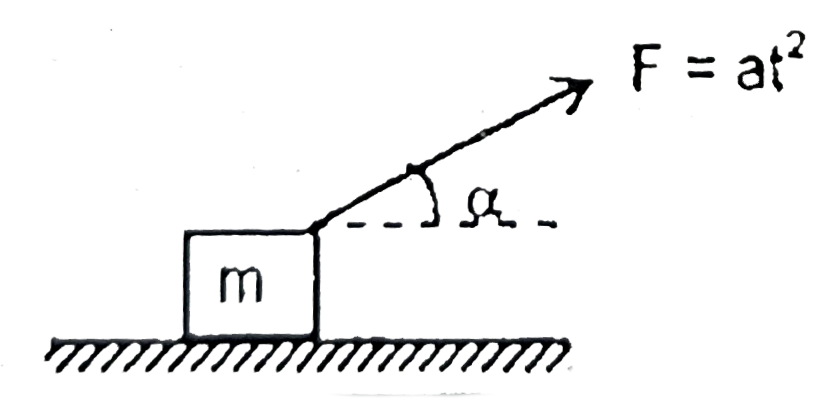
View SolutionA block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
View SolutionA ball is projected with velocity (u) at an anle α with horizontal plane. What is its speed when it makes an angle θ whith the horizontal plane ?
View SolutionAt t=0, a force F=at2 is applied to s small body of mass m at an angle α resting on a smooth horizontal plane.
View SolutionA block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
View Solution
