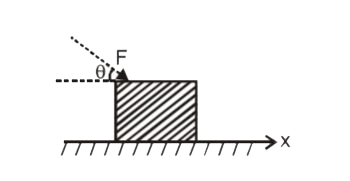
Calculate the minimum force required to drag a body of mass m, resting on a horizontal surface. The coefficient of friction between the body and the surface is $μ$ .

Text Solution

Verified by Experts

Let the applied force be F, acting at an angle $θ$ with the horizontal Fig.
$f_{2}$ = force of limiting friction, mg = weight of the body and R = normal force.
For equilibrium,
$R + F sin θ = m g or$ , R = mg - F sin $θ$
and F cos $θ = f_{s} = μ R = μ (m g - F sin θ$ )
or, F cos $θ + μ F sin θ = μ$ mg
$∴ F = \frac{μ m g}{cos θ + μ sin θ}$
Value of F will be minimum when ( cos $θ + μ sin θ$ ) is maximum.
$∴ \frac{d}{d θ} (cos θ + μ sin θ) = 0$
or , - sin $θ + μ cos θ = 0 or, tan θ = μ$
$∴ sin θ = \frac{μ}{\sqrt{1 + μ^{2}}}, and cos θ = \frac{1}{\sqrt{1 + μ^{2}}}$
$∴ F_{min} = \frac{μ m g}{\frac{1}{\sqrt{1 + μ^{2}}} + \frac{μ^{2}}{\sqrt{1 + μ^{2}}}} = \frac{μ m g}{\sqrt{1 + μ^{2}}} and θ = {tan}^{- 1} μ$

|

Updated on:21/07/2023

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is $μ$ . The force of friction between the mass and the surface is :

A $μ m g$
B $μ [m g + \frac{F}{2}]$
C $\frac{F \sqrt{3}}{2}$
D $μ [m g - \frac{F}{2}]$
Question 2 - Select One
A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
A $\frac{F - μ m g}{M}$
Bzero
Cmay be (A) or (B)
DNone of these
Question 3 - Select One
A body of mass $M$ is applying horizontal force to slide a box of mass $M_{1}$ on a rough horizontal surface The coefficient of friction between the shoe of the boy and the floor is $μ$ and that between the box and the floor is $' μ_{1}'$ In which of the following cases is it certainly not possible to slide the box ? .
A $μ < μ_{1}, M < M_{1}$
B $μ > μ_{1}, M > M_{1}$
C $μ < μ_{1}, M > M_{1}$
D $μ_{1} > μ_{1}, M < M_{1}$

CHHAYA PUBLICATION-FRICTION -CBSE SCANNER

Home
Ask Doubt
Profile