A body tied to a thread is made to revolve in a horizontal plane with a definite velocity and the thread does not snap. But when the body is made to revolve in a vertical plane, the thread snaps. How is it possible ?
Let the length of the thread be l , mass fo the body
m, velocity of revolution v and tension in the thread T when the body is rotated in the horizontal plane [Fig.1.53].

Required centripetal force for revolution,
mv2lsinθ=Tsinθ.........(1)
and mg =Tcosθ .........(2)
From equations (1) and (2) we get,
sin2θ+cos2θ=mv2lT+(mgT)2
or,T2=mv2lT+m2g2
or,T2−mv2lT+m2g2=0
∴T=mv2l±√(mv2l)2+4m2g22
∵T>0andmv2l<√(mv2l)2+4m2g2
T=12⎡⎣mv2l+√(mv2l)2+4m2g2⎤⎦
or,T=12⎡⎣mv2l+√(mv2l+2mg)2−2⋅mv2l⋅2mg⎤⎦........(3)
Now, mv2l+2mg>√(mv2l+2mg)2−2⋅mv2l⋅2mg
∴ From equation (3) ,it can be ineferred that
T<12[mv2l+(mv2l+2mg)]
or,T<(mv2l+mg)........(4)
Again, when th body is revolved in the vertical plane , tension in the thread at the lowest point of the circular path,
T.=mv2l+mg.......(5)
∴ From equation (4) and (5) we get,
T<T.
So, tension in the thread at the lowest point in the second case is greater than that in the first case, and hence, in the first case though the thread does not snap, in the second case the thread may snap.
Topper's Solved these Questions
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - EXERCISE (Multiple Choice Questions)
33 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - EXERCISE (Very short Answer Type Questions)
30 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - SECTION RELATED QUESTIONS
24 Videos
- WBCHSE QUESTION PAPER -2019BOOK - CHHAYA PUBLICATIONCHAPTER - WBCHSE QUESTION PAPER -2019EXERCISE - SECTION - II ( GROUP -D)
10 Videos
Similar Questions
A body tied to one end of a string is made to revolve in a vertical circle. Derive an expression for the velocity of the body and tension in the string at any point.
View SolutionA small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole O(figure) with a constant velocity. Find the thread tension as a function of the distance r between the body and the hole if at r=r0 the angular velocity of the thread is equal to ω0.
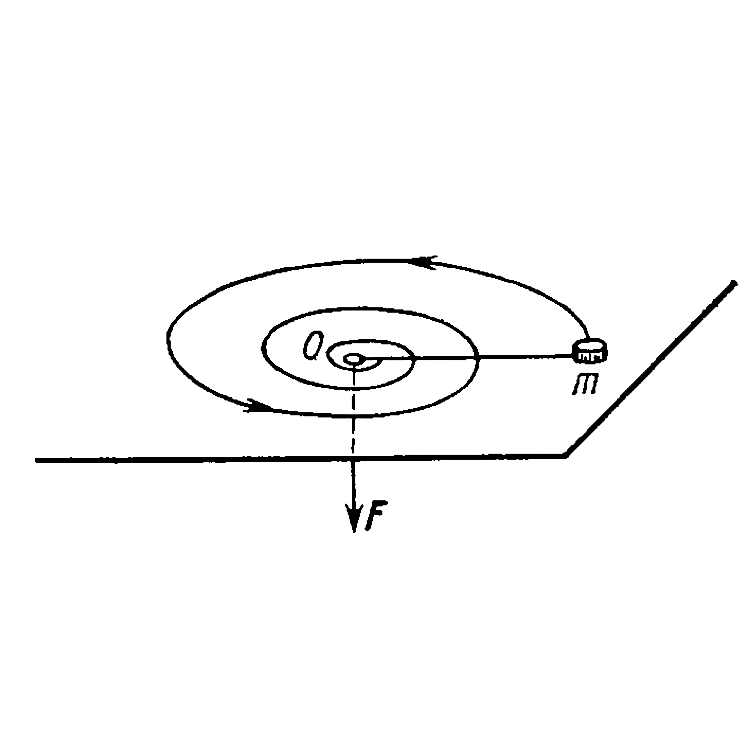
View Solution
Knowledge Check
The thread of a kite makes angle 60∘ with the horizontal plane . If the length of the thread be 80 m , then the vertical height of the kite will be
A40√3 metreB30√3 metreC80 metreD40√3 metreTwo masses M and m are attached to a vertical axis by weightless threads of combined length l . They are set in rotational motion in a horizontal plane about this axis with constant angular velocity ω . If the tensions in the threads are the same during motion, the distance of M from the axis is
AMlM+mBmlM+mCM+mMlDM+mmlA ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
Atan−1(2)Btan−1(√2)Ctan−1(12)D2tan−1(12)
A smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
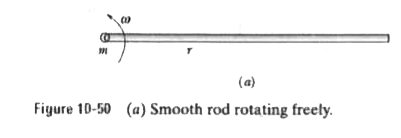
View SolutionA small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical,
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum,
(c) the angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.
View SolutionA small ball is suspended from a point O by a light thread of length l. Then the ball is drawn aside so that thread deviates through an angle θ from the vertical and set in motion in a horizontal direction at right angles to the vertical plane in which the thread is located. What is the initial velocity that has to be imparted to the ball so that it could deviate through the maximum angle π/2 in the process of motion?
View SolutionFigure shows a spool with thread wound on it placed on a smooth plane inclined at angle from horizontal. The spool has mass m, edge radius R, and is wound up to a radius r. its moment of inertia about its own axis is I. The free end of the thread is attached as shown in the figure. So that the thread is parallel to the inclined plane. T is the tension in the thread. Which of the following is correct?

View SolutionFigure shows a spool with thread wound on it placed on a smooth plane inclined at angle from horizontal. The spool has mass m, edge radius R, and is wound up to a radius r. its moment of inertia about its own axis is I. The free end of the thread is attached as shown in the figure. So that the thread is parallel to the inclined plane. T is the tension in the thread. Which of the following is correct?

View Solution
