The potential energy of a spring pendulum, with a mass m connected to it, is given by V=12kx2 (where x = displacement from the position of equilibrium and k = a constant). How does the applied force on the mass vary with displacement?Solution in Bengali
Suppose, the force applied on the mass m = F.
If V is the potential energy of the spring pendulum, then
F=−dVdx=−ddx(12kx2)=−12k⋅2x=−kx
So, the applied force F is proportional to x and acts in a direction opposite to that of x.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE
33 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
23 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SECTION RELATED QUESTIONS
8 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
Similar Questions
The motion of any hand of a clock is a (an)
View SolutionIf the time period of an SHM is 2 s, then what will be its frequency?
View SolutionEstablish the mathematical expression for simple harmonic motion.
View SolutionA solid sphere of mass m and radius r is rolling on a horizontal surface. What ratio of total energy of the sphere is:
Kinetic energy of rotation ?
Kinetic energy of translation ?
View SolutionFour bodies have been arranged at the corners of a rectangle shown in Fig. Find the centre of mass of the system.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.
View SolutionA physics student writes the elastic potential energy stored in a spring as U=1/2KL^(2)+1/2Kx^(2), where L is the natural length of the spring, x is extension or compression in it and K is its force constant. A block of mass M travelling with speed V hits the spring and compresses it. Find the maximum compression caused.
View SolutionIf the mass of a spring, m, is not negligible but small compared to the mass M suspended from it, show that the period of oscillations is given by T= 2pisqrt((M+m/3)//k) , where k is the force constant of the spring. [Hint: If x and v be the instaneous displacement and velocity of the lower end, then the displacement of an element at a distance z from the fixed end is xz/l and velocity zv/l. The kinetic energy of the spring = (int_(0)^(t))1/2(mdz/l)z^(2)v^(2)/l^(2) = 1/6 mv^(2) Total energy of the system = 1/6mv^(2)+1/2Mv6(2) + 1/2kx^(2) = a constant. Differentiate anmd find T.]
View SolutionOn applying a force F the mass M is displaced vertically down by from equilibrium position, Find the force F in terms of the force constant k of the spring and displacement y for the cases (A) and (B) as shown in
View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionTwo springs of spring constant k_(1)and k_(2) are connected by a mass m as shown in the figure. Under negligible friction, if the mass is displaced by small amount x from its equilibrium position and released, the period of oscillation is
View SolutionA particle of mass m oscillates with a potential energy U=U_(0)+alpha x^(2) , where U_(0) and alpha are constants and x is the displacement of particle from equilibrium position. The time period of oscillation is
View SolutionA mass 1 kg is attaced to the hook of a spring and the spring is suspended vertically from a ceiling (see Fig. 5.12a). The spring is displaced from its equilibrium position by a distance x. The spring constant of the spring is 2.0×102 N/m. Calculate the displacement x.
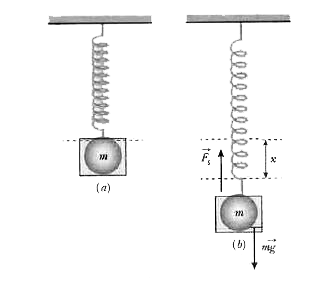
Figure 5-12 (a) Mass of 1 kg attached to a spring is suspended vertically. (b) Spring displace from equilibrium position by a distance x.
View Solutionएक m द्रव्यमान का ब्लॉक एक k स्प्रिंग नियतांक की स्प्रिंग से चित्रानुसार जुड़ा है। ब्लॉक में महत्तम विस्थापन है
View Solution
