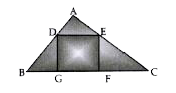
In the given figure , DEFG is a square and ∠BAC=90∘ prove that (i) △AGF~△DBG (ii)△AGF~△EFC
Text Solution
(i) Since □DEFG is a square
GF||BC
⇒∠2=∠4and∠6=∠9 ( corresponding ∠s)
Now in △AGFand△DBG
∠5=∠1 ( each 90∘)
∠4=∠2 (corrersponding ∠s)
 ( AA corollary Hence proved.)
( AA corollary Hence proved.)
(ii) In △AGFand△DBC,
∠5=∠8(each90∘)
∠4=∠2 ( corresponding ∠s)
 ( AA corollary)
( AA corollary)
(iii) since △AGF~△DBG [proved in (i)]
and △AGF~△EFC [ proved in (ii)]
△AGF~△DBG~△EFC Hence proved.
Now since 
DBEF=DGEC (corrsponding sides of similar △s are proportional)
⇒DG×EF=BD×EC
⇒DE×DE=BD×EC ( DG= FE= DE being the sides of sqaure)
DE2=BD×EC
BUT
If we have to prove only the fourth part i.e. prove that DE2=BD×EC then no need to prove first two parts.
For DE2=BD×EC , we need to prove two △s similar which contains DE, BD and EC.
Obviously, these are △GBDand△FEC.
∠1=∠8 (each 90∘)Searching for second AnglesAs we know that ∠5=90∘Also, ∠2+∠9=90∘(angle sum property)....(1)∴ Also Since ∠1=90∘∠2+∠3=90∘(angle sum property)...(2)∴From (1) and (2) , We get ⇒ ∠2+∠3=∠2+∠9 (each90∘)⇒ ∠3=∠9
Now in △GBDand△FEC.
∠1=∠8(each90∘)
∠3=∠9 ( just proved)
 ( AA corollary)
( AA corollary)
DG×EF=BD×EC
DE×DE=BD×EC ( DG = EF = DF , sides of a square)
⇒DE2=BD×EC Hence proved.
|
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In the given figure, the measure of ∠BAC is,
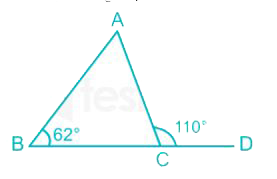 A56∘B58∘C62∘D48∘
A56∘B58∘C62∘D48∘
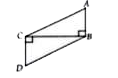
In the given figure, Ab = CD and ∠ABC=∠DCB=90∘. Prove that AC = DB.
View SolutionIn the figure, DEFG is a square and ∠BAC=90∘. Prove that
(A) ΔAGF~ ΔDBG
(B)ΔAGF~ΔEFC
(C) ΔDBG~ΔEFC

View SolutionIn the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
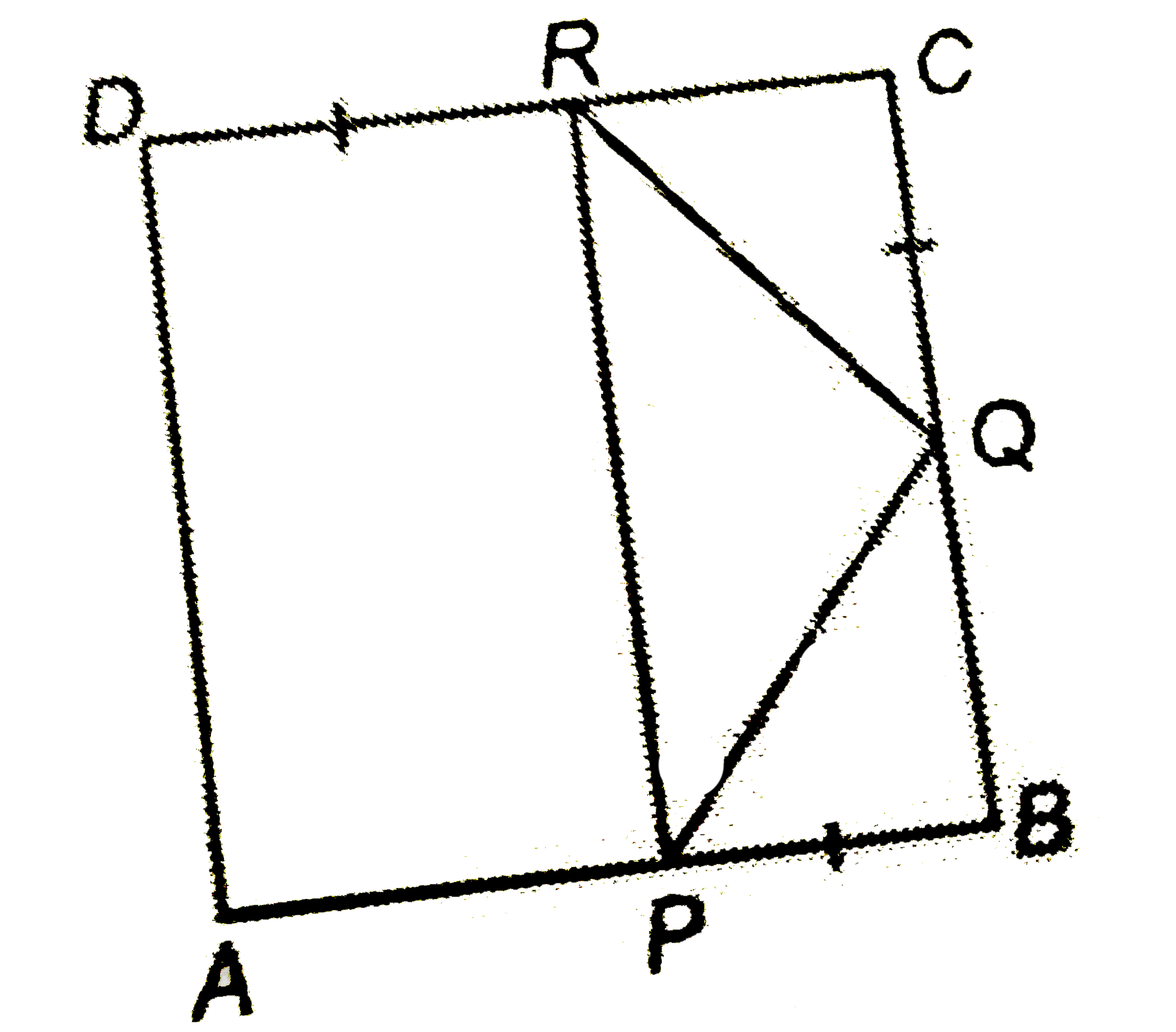
View SolutionIn the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘

View SolutionIn fig.7.84, DEFG is a square and ∠BAC=90°. Prove that:
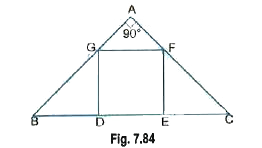
(i) ΔAGF~ΔDBG (ii) ΔAGF~ΔEFC(iii) ΔDBG~ΔEFC (iv) DE2=BD×EC
View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.

View SolutionIn the given figure, ∠BAC=∠CDBand∠ACB=∠DBC. Prove that AC = DB.

View Solution