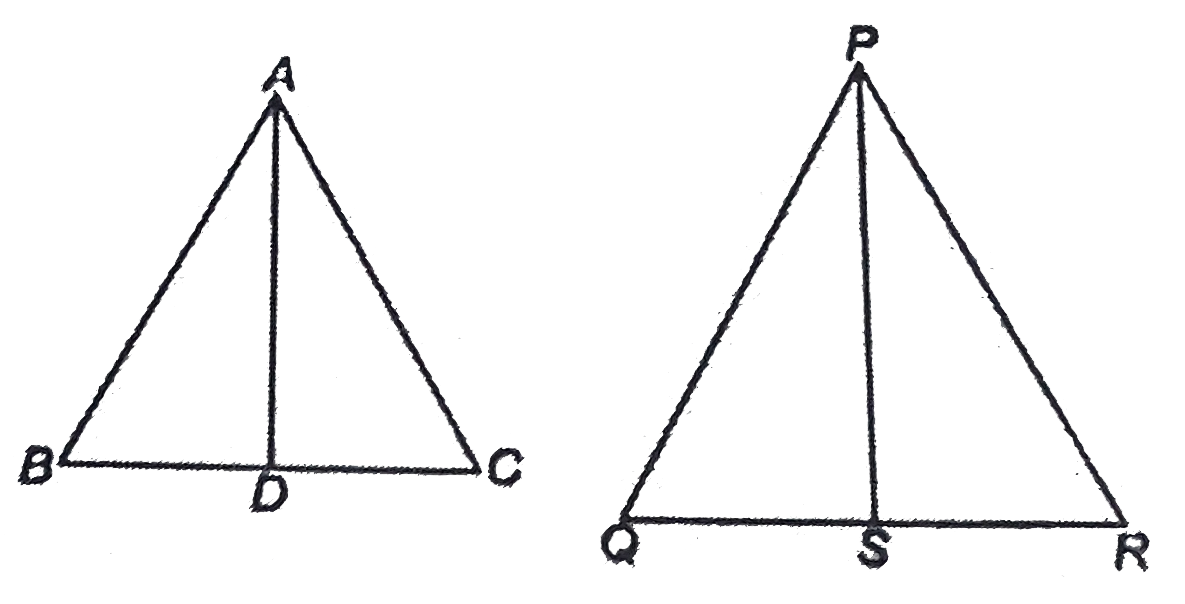
If two sides and a median bisecting one of these sides of a triangle are respectively proportional to the two sides and corresponding median of another triangle; then triangle are similar.
△ABCand△PQR in which AD and PS are the medians such that.
ABPQ=BCQR=ADPS
To prove : △ABC~△PQR
Proof: since, ABPQ=BCQR=ADPS
⇒ABPQ=2BD2QS=ADPS ( AD and PS are the medians)
⇒ABPQ=BDQS=ADPS
△ABD~△PQS (SSS criterion of similarity)
∠B=∠Q ( corresponding ∠s of similar triangles are equal)
Now in △ABCand△PQR
ABPQ=BCQR (given)
and ∠B=∠Q
△ABC~△PQR (SAS criterion of similarity) Hence proved.
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
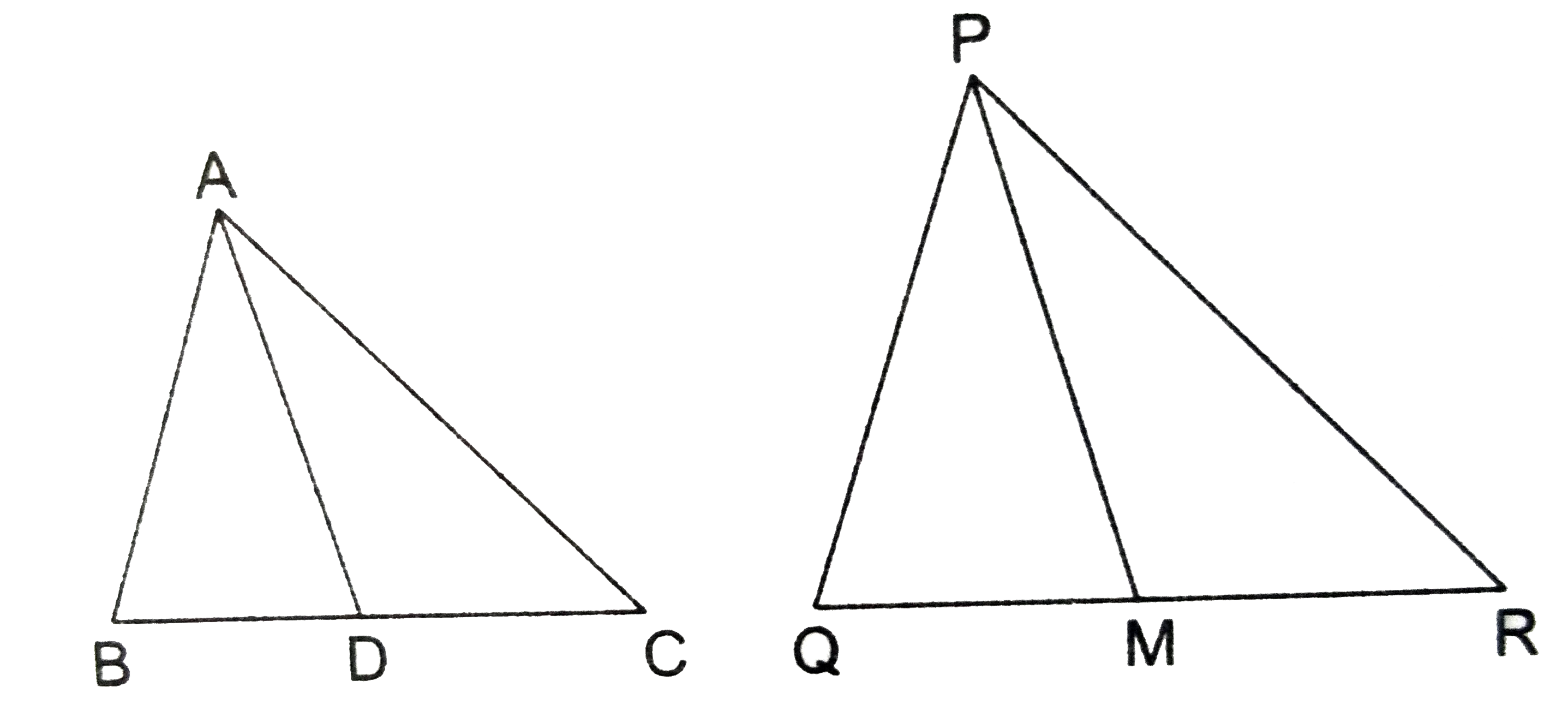
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
View SolutionIs it true to say that, if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reason for your answer.
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
View SolutionTwo sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionThe areas of the two similar triangles are in the ratio of the square of the corresponding medians.
View SolutionIf corresponding sides of two similar triangles are in the ratio 4 : 5 , then corresponding medians of the triangles are in the ratio 4:k . Find K .
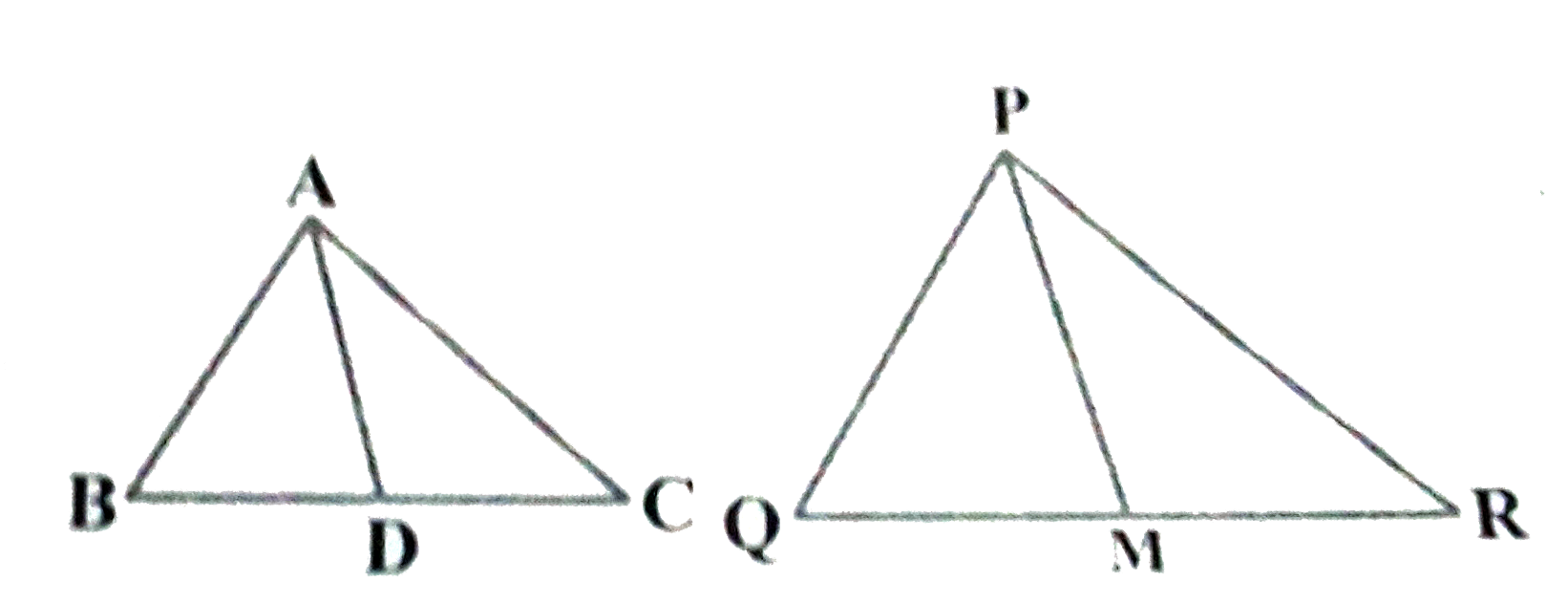
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
View SolutionProve that Two right triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other triangle.
View SolutionTheorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
View Solution
