In triangle ABC, ∠A=90∘ , CA= AB and D is a point on AB porduced. Prove that :
DC2−BD2=2AB.AD
To prove that DC2−BD2=2AB⋅AD in triangle ABC where ∠A=90∘, CA=AB, and D is a point on AB produced, we can follow these steps:
1. Draw Triangle ABC:
- Draw triangle ABC such that ∠A=90∘. Let CA=AB=x (since CA=AB).
2. Identify Point D:
- Extend line AB to point D such that D is on the line produced from AB.
3. Apply Pythagorean Theorem in Triangle CAD:
- In triangle CAD, apply the Pythagorean theorem:
CD2=CA2+AD2
4. Express AD in terms of AB and BD:
- Since AD=AB+BD, substitute this into the equation:
CD2=CA2+(AB+BD)2
5. Expand the Equation:
- Expand (AB+BD)2:
CD2=CA2+AB2+2AB⋅BD+BD2
6. Substitute CA with AB:
- Since CA=AB, we can replace CA2 with AB2:
CD2=AB2+AB2+2AB⋅BD+BD2
- This simplifies to:
CD2=2AB2+2AB⋅BD+BD2
7. Apply Pythagorean Theorem in Triangle CDB:
- Now, apply the Pythagorean theorem in triangle CDB:
BC2=BD2+CD2
8. Express BC in terms of AB:
- Since CA=AB, we can find BC2 as:
BC2=CA2+AB2=AB2+AB2=2AB2
9. Combine the Equations:
- From the previous steps, we have:
CD2−BD2=2AB2+2AB⋅BD
- Substitute BC2 into the equation:
CD2−BD2=2AB⋅AD
10. Final Result:
- Thus, we have proved that:
DC2−BD2=2AB⋅AD
- Draw triangle ABC such that ∠A=90∘. Let CA=AB=x (since CA=AB).
- Extend line AB to point D such that D is on the line produced from AB.
- In triangle CAD, apply the Pythagorean theorem:
CD2=CA2+AD2
- Since AD=AB+BD, substitute this into the equation:
CD2=CA2+(AB+BD)2
- Expand (AB+BD)2:
CD2=CA2+AB2+2AB⋅BD+BD2
- Since CA=AB, we can replace CA2 with AB2:
CD2=AB2+AB2+2AB⋅BD+BD2
- This simplifies to:
CD2=2AB2+2AB⋅BD+BD2
- Now, apply the Pythagorean theorem in triangle CDB:
BC2=BD2+CD2
- Since CA=AB, we can find BC2 as:
BC2=CA2+AB2=AB2+AB2=2AB2
- From the previous steps, we have:
CD2−BD2=2AB2+2AB⋅BD
- Substitute BC2 into the equation:
CD2−BD2=2AB⋅AD
- Thus, we have proved that:
DC2−BD2=2AB⋅AD
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Very Short Questions9videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Short Questions10videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6c11videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
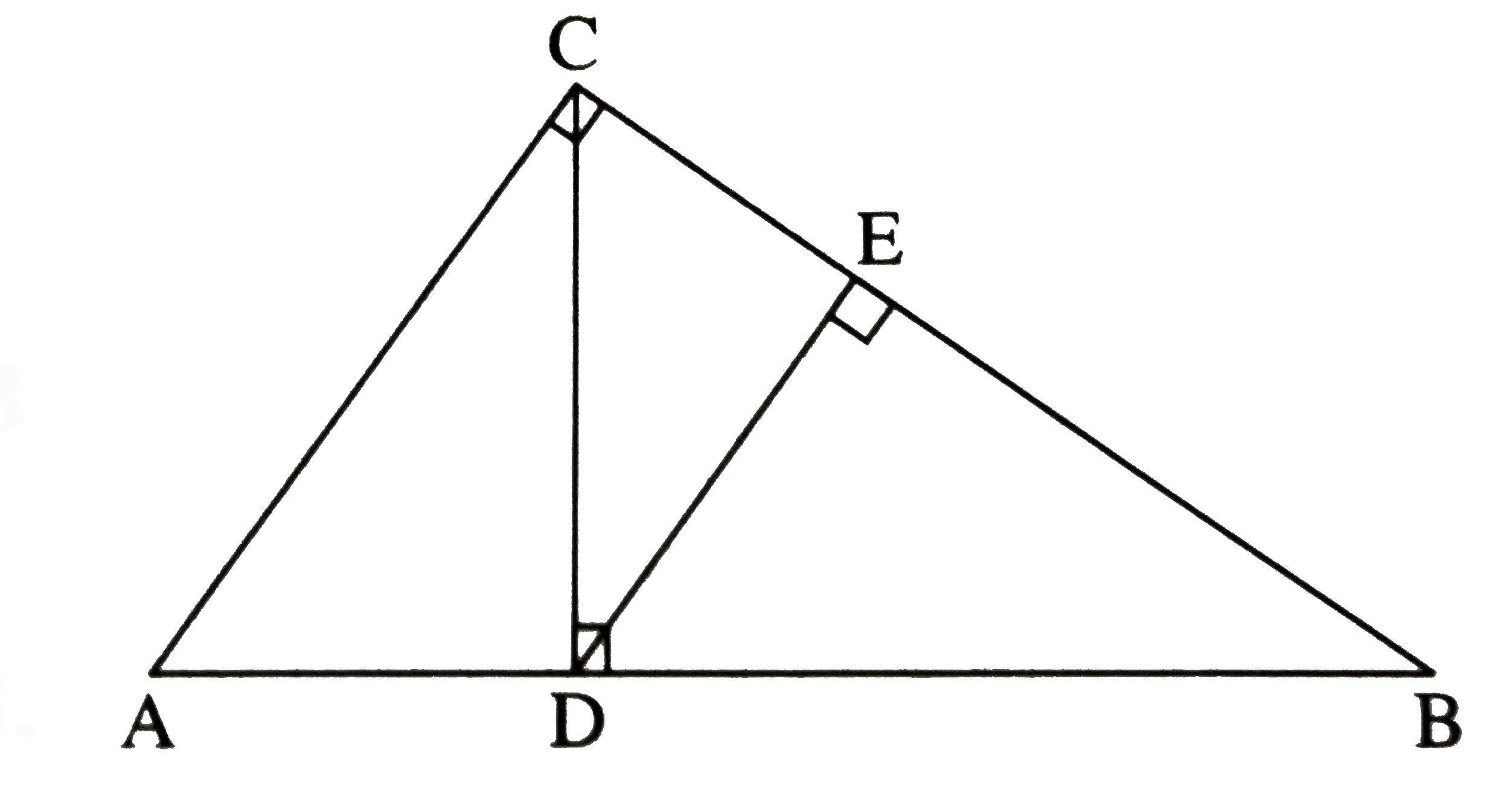
In △ ABC ,
∠ACB=90∘ ,
CD⊥AB and
DE⊥CB
Prove that CD2×AC=AD×AB×DE .
 View Solution
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn △ABC, AB=AC and D is any point on BC, prove that AB2−AD2=BD.CD
View SolutionIn an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View SolutionIn right-angled triangle ABC in which ∠C=90∘ , if D is the mid-point of BC , prove that AB2=4 AD2−3 AC2 .
View SolutionIn triangle ABC , ∠BAC=90∘ and AB=AC. Seg AP is perpendicular to side BC. D is any point on side BC. Prove that 2(AD)2=(BD)2+(CD)2
View SolutionΔABC is an isosceles right angled triangle having ∠C=90∘. If D is any point on AB, then AD2+BD2 is equal to
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
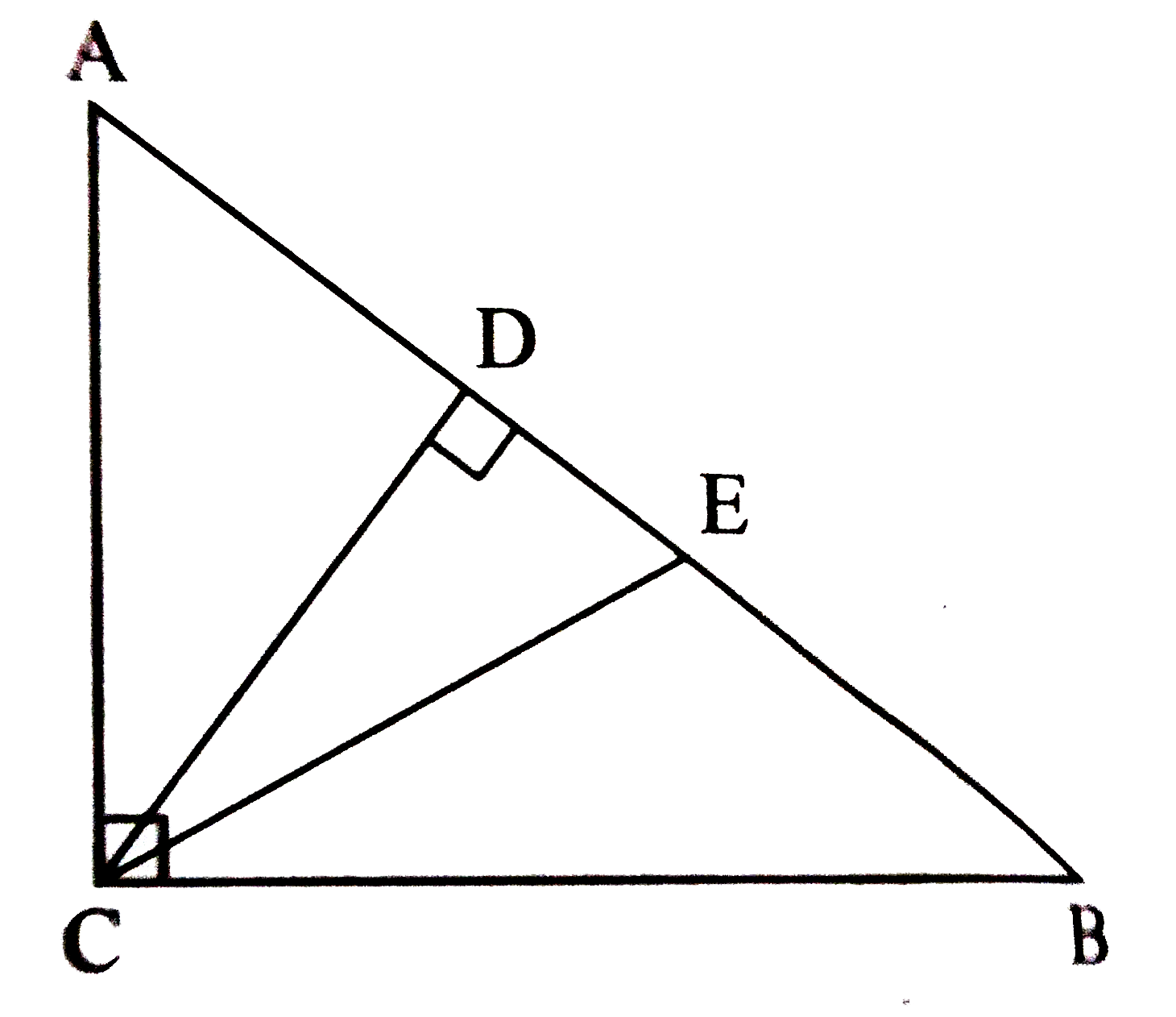
AB2−BD2=AC2−CD2View SolutionIn ΔABC,∠ACB=90∘, seg CD⊥ side AB and seg CE is angle bisector of ∠ACB
Prove : ADBD=AE2BE2
 View Solution
View Solution

