in the given figure, AB and BC are two chords of
the circle with Centre O, where
∠BAO = 50°, ∠BCO = 35°, then ∠AOC
is equal to
A)170°
b)70°
c)150°
d)None of these
Step by step video & image solution for in the given figure, AB and BC are two chords of the circle with Centre O, where /_BAO = 50°, /_BCO = 35°, then /_AOC is equal to A)170° b)70° c)150° d)None of these by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
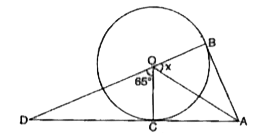 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘In the given figure, O is the centre of a circle , AB is a chord and AT is the tangent at A. If ∠AOB=100∘ then ∠BAT is equal to
A40∘B50∘C90∘D100∘
In the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.

View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=50∘ then find ∠AOC
View SolutionIn the given figure, O is the centre of the circle.

Name all chords of the circle.
View SolutionIn the figure, BC is a chord of the circle with centre o and A is a point on the minor are BC. Then ∠ABC−∠OBCis equal to
View SolutionAB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
View Solution