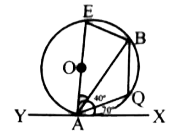
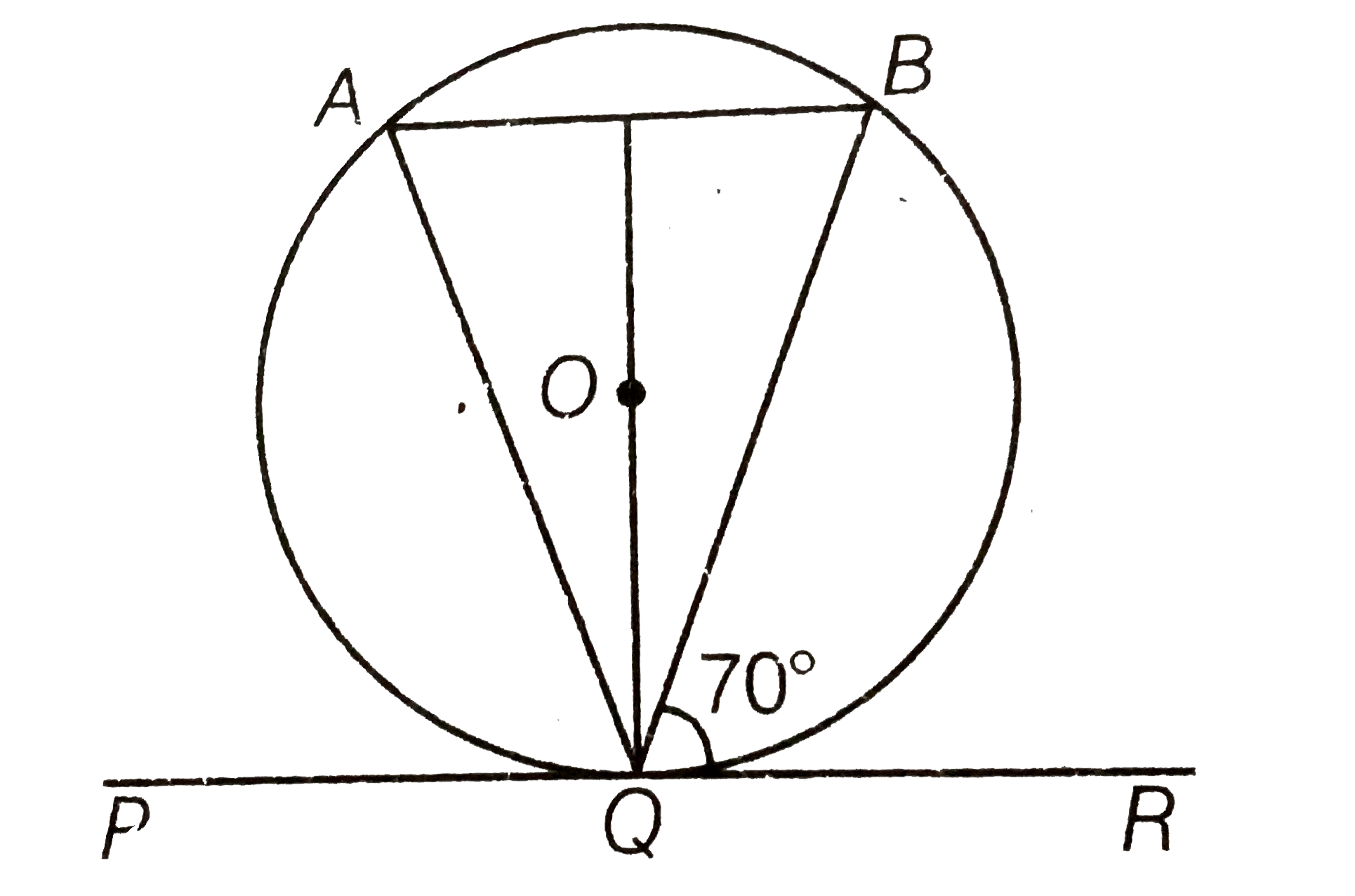
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR=70∘ then ∠AQB is equal to
A
20∘
B
40∘
C
35∘
D
45∘
Video Solution
Text Solution
The correct Answer is:B
Given, AB||PR
∴∠AQB=∠BQR=70∘ [alternate angles]
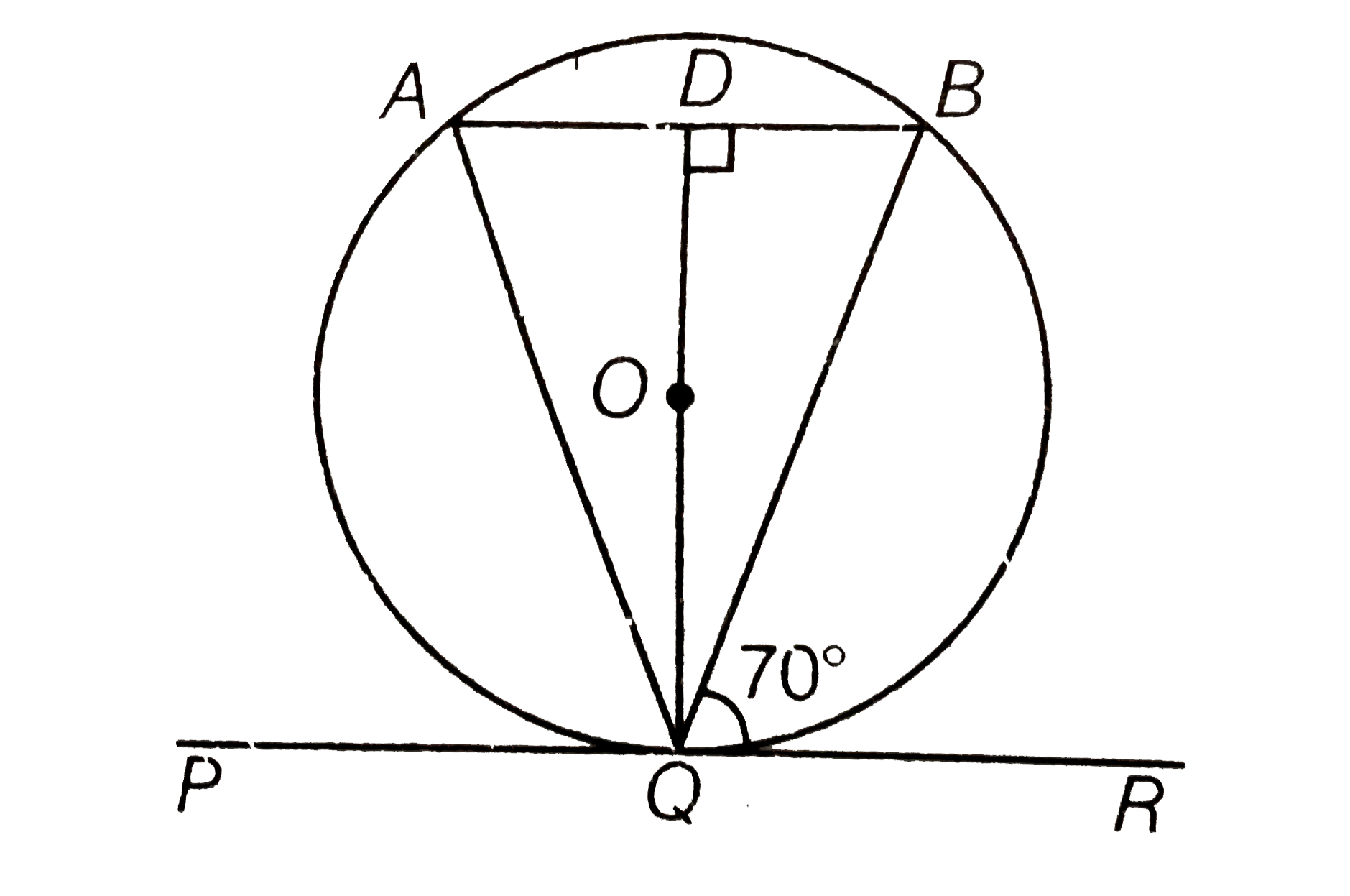
Also, QD is perpendicular to AB and QD bisects AB.
In ΔQDAandΔQDB, ∠QDA=∠QDB [each 90∘]
AD=BD
QD=QD [common side]
∴ΔADQ=ΔBDQ [by SAS similarity criterion]
Then ∠QAD=∠QBD [CPCT.....(i)]
Also ∠ABQ=∠BQR [altermat interior angle]
∴∠ABQ=70∘ [∵∠BQR=70∘]
Hence, ∠QAB=70∘ [from Eq. (i)]
Now, in ΔABQ, ∠A+∠B+∠Q=180∘
⇒∠Q=180∘−(70∘+70∘)=40∘
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABC is tangent to the circle at point B whose centres is O,PQ is a chord parallel to AC and ∠QBC=60∘, then ∠QBP is equal to
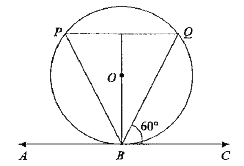 A30∘B60∘C90∘D80∘
A30∘B60∘C90∘D80∘ - Question 2 - Select One
In figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
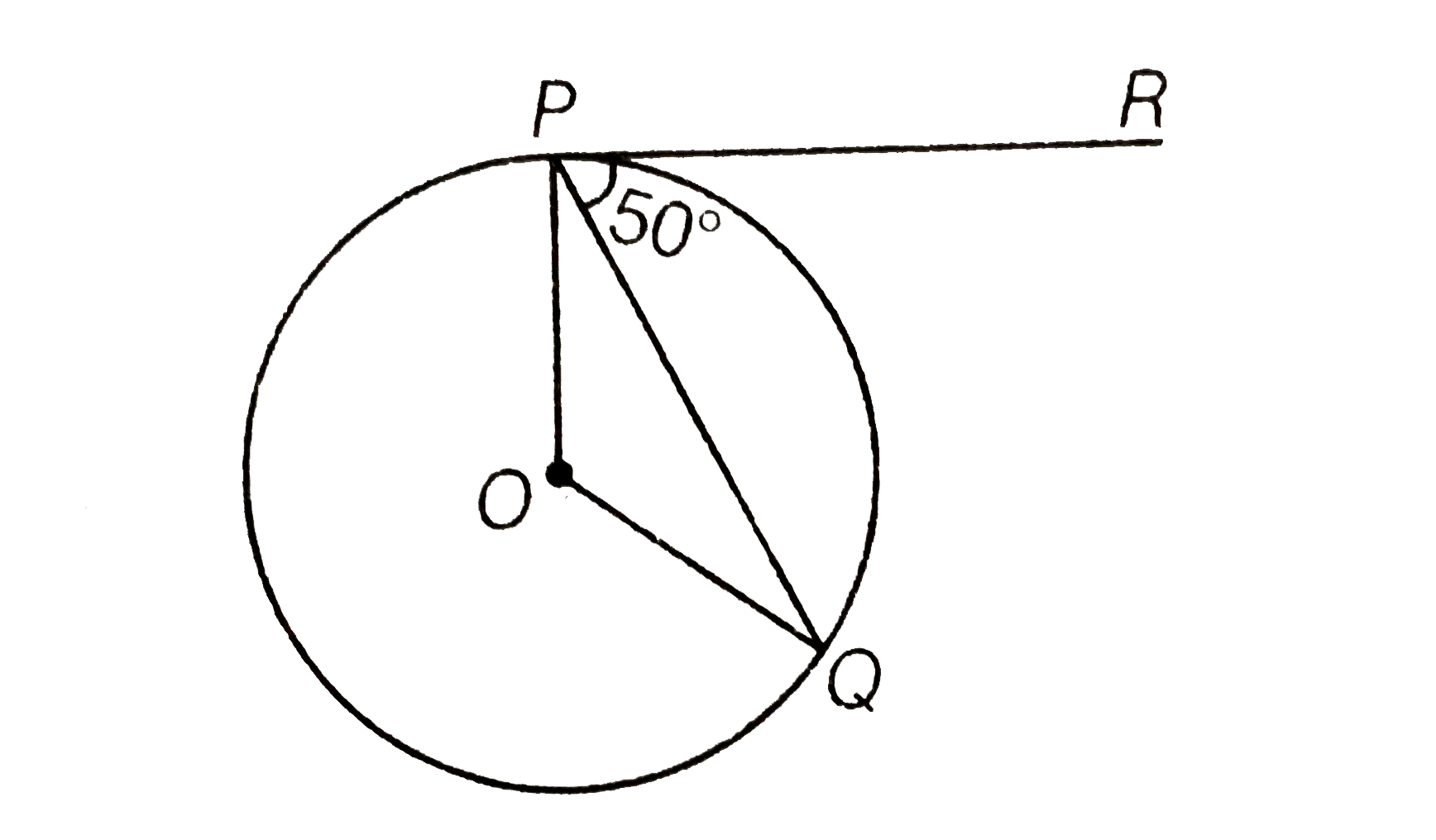 A100∘B80∘C90∘D75∘
A100∘B80∘C90∘D75∘ - Question 3 - Select One
In figure PR is tangent to the circle at P and O is the centre of the circle. The value of ∠POQ is
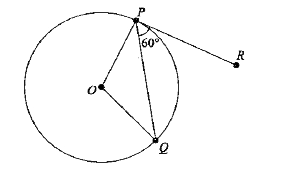 A110∘B100∘C120∘D90∘
A110∘B100∘C120∘D90∘
In the given figure ,'O is the centre of circle ,PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ ,then ∠POQ is equal to :
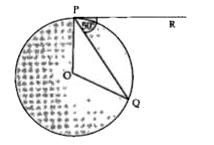 View Solution
View SolutionAB and CD are equal chords of a circle whose center is O,
View SolutionIn the figures, PQ and PR are tangents to the circle with centre O. Find RSQ , RTQ , and RˆPQ
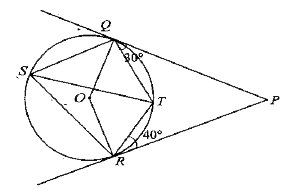 View Solution
View SolutionIn Figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If angle POQ = 70°, then angleTPQ is equal to
View SolutionIn the figure, O is the centre of the circle . ∠PQR is equal to
 View Solution
View Solution