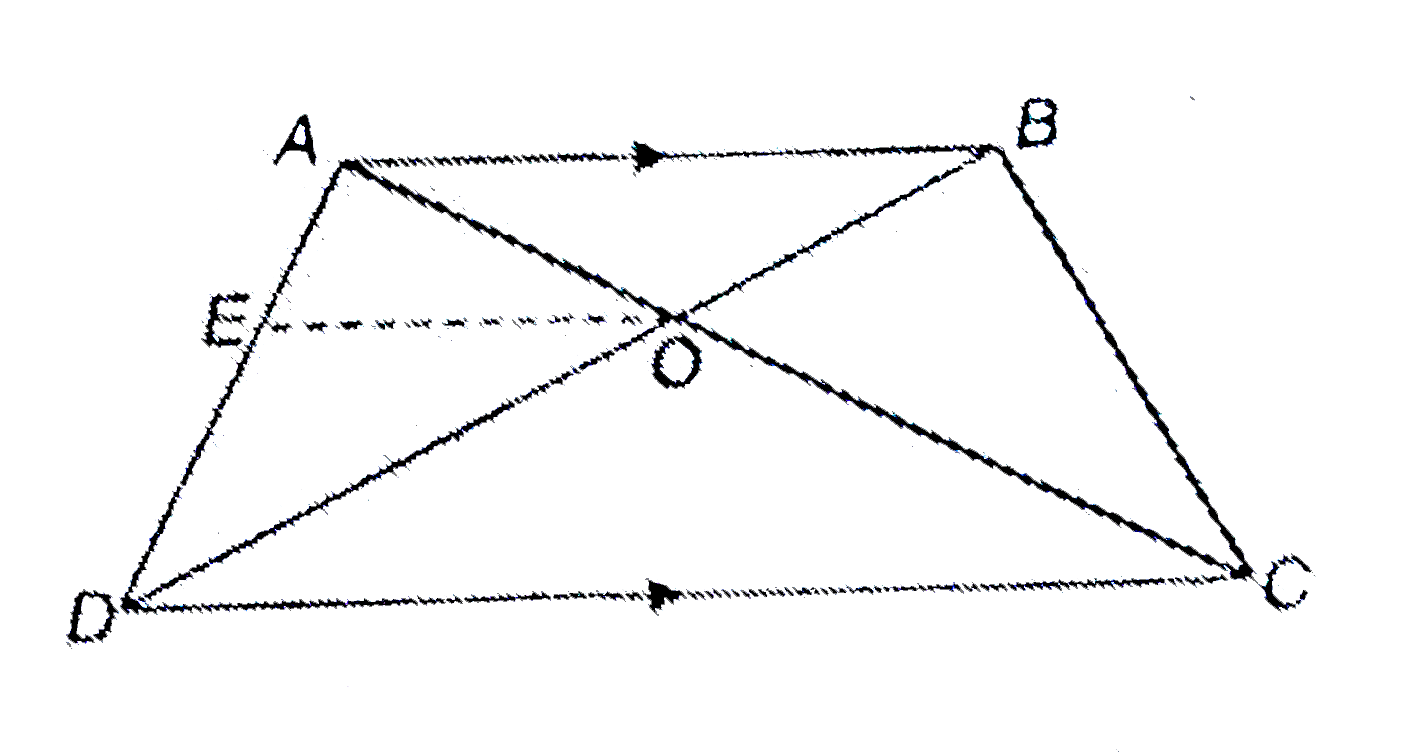
In a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
Let AC and BD intersect at O (origin)
According to the question →a.→b=0
Also AB||CD
(μ→a−λ→b)∣∣(→a−→b)
⇒μ=λ
LetAD.BC≥AB.CD
⇒∣∣λ→b−→a∣∣∣∣μ→a−→b∣∣|≥|(→b−→a)∣∣∣(λ→b−μ→a)∣∣
or(λ2b2+a2)(μ2a2+b2)≥(b2+a2)(λ2b2+μ2a2)
orλ2μ2a2b2+a2b2≥λ2a2b2+μ2b2a2
or(λ92)−1)(μ2−1)≥0
or(λ2−1)2≥0 which is true.
Hence, AD. BC ≥ AB. CD

Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Single Question)28videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Multiple Question)11videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.318videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises1316videos
CONIC SECTIONS
- BOOK - CENGAGECHAPTER - LIMITS AND DERIVATIVESEXERCISE - Solved Examples And Exercises320videos
LIMITS AND DERIVATIVES
Similar Questions
In a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn a quadrilateral ABCD it is given tghat AB∣∣CD nad the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn cyclic quadrilateral ABCD, AD∣∣BC. Prove that AB = CD.
View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).View SolutionIn a quadrilateral ABCD, show that (AB+BC+CD+DA)<2(BD+AC).
View SolutionIn quadrilatcal ABCD, prove that AB+BC+CD+AD<2(BD+AC)
View SolutionIn a trapezium ABCD , it is given that AB∣∣CDandAB=2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB)=84cm2. Find ar(ΔCOD)
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
 View Solution
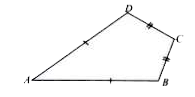
View SolutionIn quadrilateral ABCD, AB ||CD and AD= BC, prove that ∠A=∠B.
View SolutionIn quadrilateral ABCD, AB = AD and BC = CD. Show that ∠ABC=∠ADC.
 View Solution
View Solution

