is regular tetrahedron in which is the circumcentre of and E is the midpoint of edge Prove that is equal to half the edge of tetrahedron.
Let
since is equilateral, the circumecenters, triangle coincide with the centroid, therefore,
Since, we have,
or

Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Single Question)28videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Multiple Question)11videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.318videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises1316videos
CONIC SECTIONS
- BOOK - CENGAGECHAPTER - LIMITS AND DERIVATIVESEXERCISE - Solved Examples And Exercises320videos
LIMITS AND DERIVATIVES
Similar Questions
OABC is regular tetrahedron in which D is the circumcentre of OAB and E is the midpoint of edge AC. Prove that DE is equal to half the edge of tetrahedron.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn Figure, AD is the median and DE∣∣AB . Prove that BE is the median.
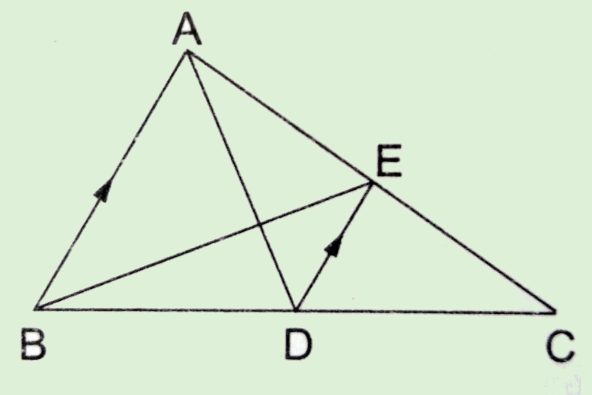 View Solution
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIF OABC is a tetrahedron where O is the origin and A,B and C have respective positions vectors as ¯a,¯band¯c then prove that the circumcentre of the tetrahedron is (¯a)2(¯bׯc)+(¯b)2(¯cׯa)+(¯c)2(¯aׯb)2[¯a¯b¯c]
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
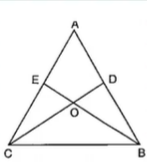 View Solution
View SolutionOABC is a tetrahedron D and E are the mid points of the edges −−→OA and −−→BC. Then the vector −−→DE in terms of −−→OA,−−→OBand−−→OC
View SolutionRegular tetrahedron a tetrahedron whose all the edges are of equal length is called a regular tetrahedron.
View Solution

