A particle is at rest at x=a. A force vecF=(b)/(x^(2))veci begins to a

A particle starts from rest x = - 2.25 m and moves along the x - axis with the v - t graph as shown. The time when the particle crosses the origin is :

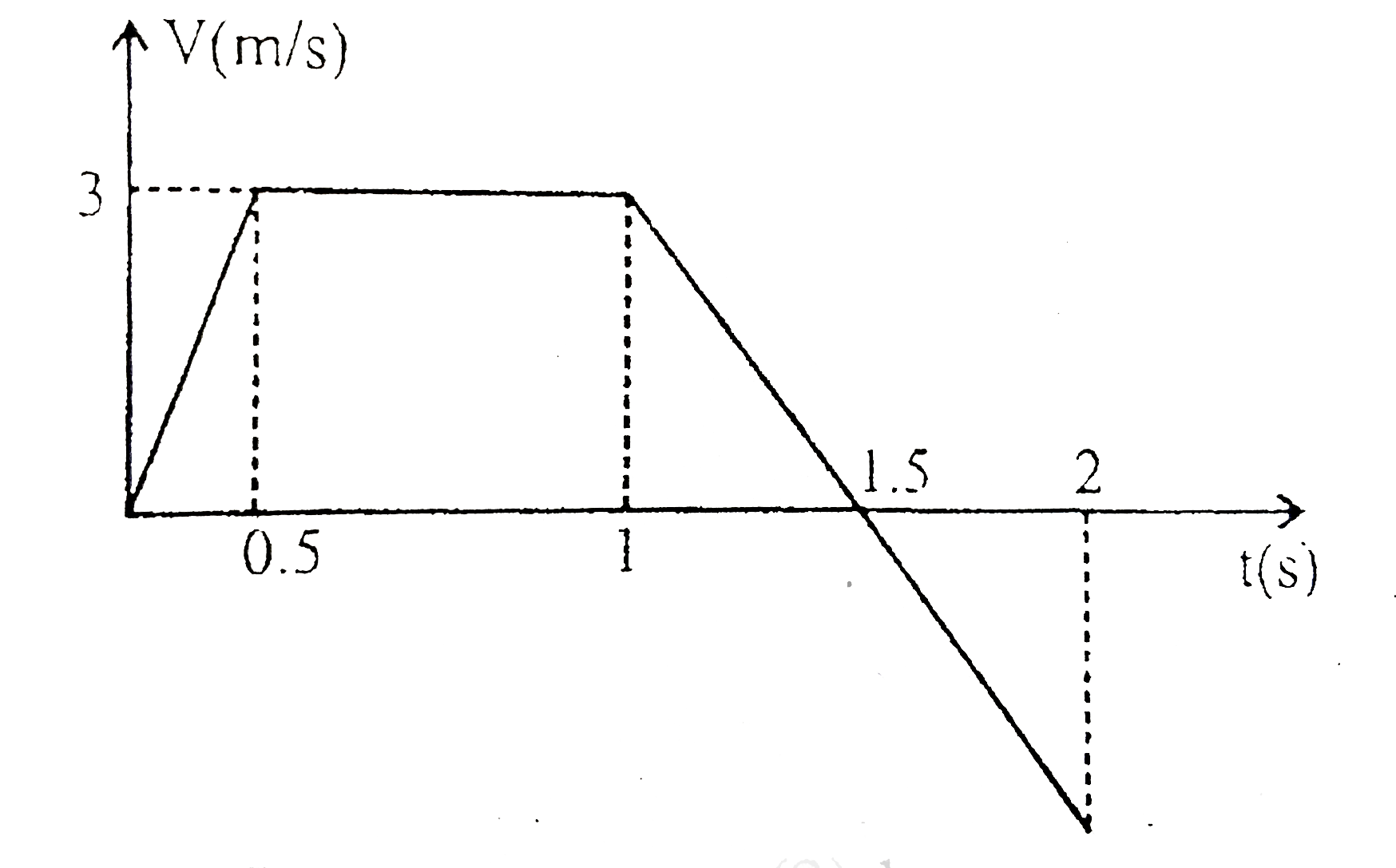A0.5 s
B1 s
C1.5 s
D2 s
A particle is projected with velocity $V_{0}$ along axis x . The deceleration on the particle is proportional to the square of the distance from the origin i.e., $a = ω x^{2} .$ distance at which the particle stops is
A ${(\frac{3 v_{0}^{2}}{2 α})}^{\frac{1}{2}}$
B ${(\frac{2 v_{0}}{3 α})}^{\frac{1}{2}}$
C ${(\frac{2 v_{0}^{2}}{3 α})}^{\frac{1}{2}}$
D ${(\frac{3 v_{0}^{2}}{2 α})}^{\frac{1}{3}}$
A particle of mass m moves on the x-axis under the influence of a force of attraction towards the origin O given by $F = - \frac{k}{x^{2}} ˆ i$ . If the particle starts from rest at x = a. The speed of it will attain to reach at distance x from the origin O will be
A $\sqrt{\frac{2 k}{m}} {[\frac{x - a}{a x}]}^{1 / 2}$
B $\sqrt{\frac{2 k}{m}} {[\frac{a + x}{a x}]}^{1 / 2}$
C $\sqrt{\frac{k}{m}} [\frac{a x}{x - a}]$
D $\sqrt{\frac{m}{2 k}} {[\frac{a - x}{a x}]}^{1 / 2}$

A particle is at rest at $x = a$ . A force $\to F = \frac{b}{x^{2}} \to i$ begins to act on the particle. The particle starts its motion, towards the origin, along X - axis. Find the velocity of the particle, when it reaches a distance x from the origin.