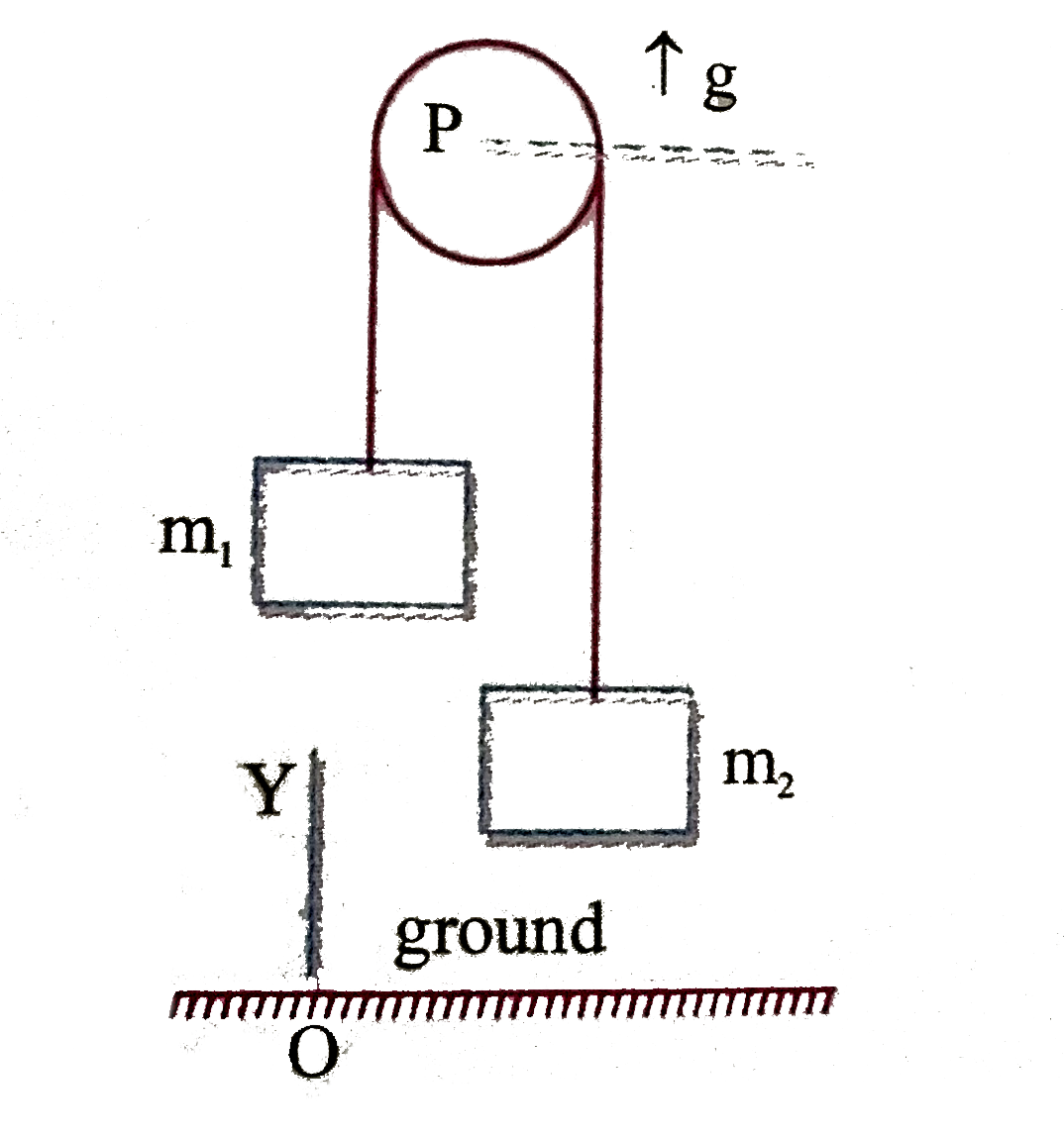
Two masses m1andm2 are connected by a light string passing over a fixed pulley as shown. The system is suspended in a vertical plane. Find the tension in the string connecting m1andm2 and acceleration of masses if m1=3kg and m2=5kg. Also find the tension in the rope connecting the centre of pulley to the ceiling.

As m2 is heavier, it movs down and m1 moves up. Let the magnitude of acceleration = a (same for both as they are connected by same string).

Let T be the tension in the string.
Draw the force diagrams of both mass
(i) Net force in the direction of acceleration =m2a
⇒ T−m1g=m1a ...(i)
(ii) Net force in the direction of acceleration =m2a
⇒ m2g−T=m2a ....(ii)
Adding (i) and (ii), we get
m2g−m1g=m1a+m2a
⇒a=m2−m1m2+m1gandT=2m1m2m2+m1g
⇒ a=g4=2.45m/s2andT=36.75N
Free body diagram of pulley

T0= tension in the rope tied to the centre of pulley
As pulley is massless, so net force on it is zero.
T0=T+T=2T⇒T0=2×36.75=73.5N
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EVALUATE YOURSELF - 1
11 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EVALUATE YOURSELF - 2
11 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
The tension in the string connected between blocks is

View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View Solution
Knowledge Check
Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2gTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
ABoth a and T will changeBa will change but T will remain unchangedCT will change but a will remain unchangedDNone of these will changeTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
A3m1m2m1+m2gBm1+m24m1m2gC2m1m2m1+m2gDm1m2m1+m2g
Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be

View Solution
