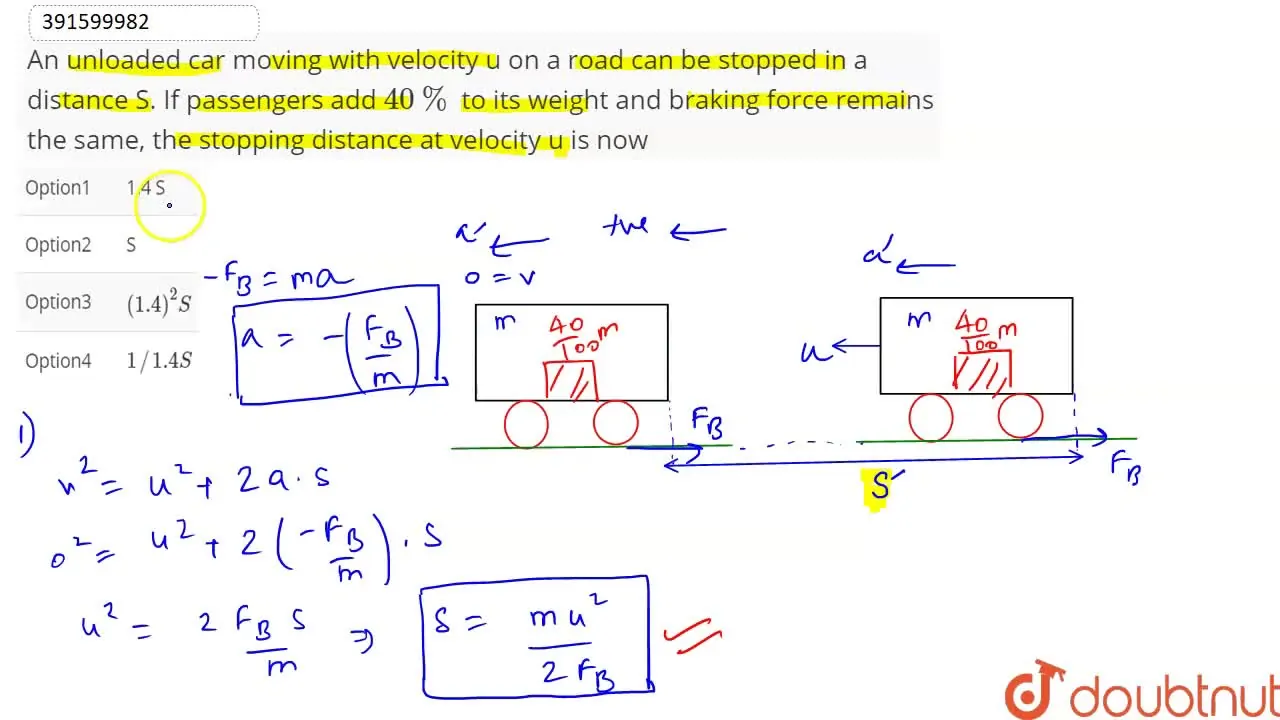
An unloaded car moving with velocity u on a road can be stopped in a distance S. If passengers add 40% to its weight and braking force remains the same, the stopping distance at velocity u is now
1.4 S
S
(1.4)2S
1/1.4S
The correct Answer is:A
Let braking force is fand mass of unloaded car is m, when car is unloaded
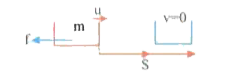
⇒a=fm=constant
⇒02=u2−2(fm)S
⇒S=mu22f
When car is loaded
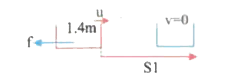
⇒a=f1.4m
Related Playlists
- BOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - III20videos
LAW OF MOTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q13videos
MATHEMATICAL REVIEW & PHYSICAL WORLD
Similar Questions
A taxi without any passengers, moving on a frictionless horizontal road, with a velocity u can be stopped in a distance d. Now the passengers and 40% to its weight. What is the stopping distance at veolcity u, if the retardation remains the same?
View SolutionAn unloaded bus can be stopped by applying brakes on straight road after covering distance x. Suppose. The passengers add 40% of its weight as the load the braking force remains same. How far will the bus go after the application of the breakes? (Velocity of bus is same in both the cases)
View SolutionAn unloaded bus can be stopped by applying brakies on straight road after covering a distance x. Suppose, the passenger add 50% of its weight as the load and the braking force remains unchanged, how far will the bus go after the application of the brakes ?(Velocity of bus in both case is same) (Consider negligible friction):-
View SolutionA car moving with a velocity of 40 km/h can be stopped by brakes after travelling at least 5 m. If same car moves at a speed of 80 km/h the minimum stopping distance is
View SolutionA car moving with a velocity of 20ms−1 is stopped in a distance of 40m. If the same car is travelling at double the velocity, the distance travelled by it for same retardation is
View SolutionA car moving with a speed of 40 km/hr can be stopped by applying brakes after at least 2 m. If the same car is moving with a speed of 80 km/hr. What is the stopping distance ?
View SolutionA car moving with speed v on a straight road can be stopped with in distance d on applying brakes. If same car is moving with speed 3v and brakes provide half retardation, then car will stop after travelling distance
View SolutionA car moving with a speed of 50 km/h, can be stopped by brakes after atleast 6 m. If the same car is moving at a speed of 100 km/h, the minimum stopping distance is
View SolutionAn automobile travelling with a speed 60km/h , can brake to stop within a distance of 20m . If the car is going twice as fast i. e. , 120km/h, the stopping distance will be
View SolutionA car moving with a velocity v is stopped within a distance x by applying a retarding force F. If the speed of the car is doubled, then the force required to stop the car with the same distance is
View Solution