Two blocks of equal mass m are connected by an unstreched spring and the system is kept at rest on a frictionless horizontal surface . A constant force F is applied on one of the blocks pulling it away from the other as shown in figure .

(a) Find the position of the centre of mass at time t .
(b) If the extension of the spring is x0 at time t , find the displacement of the two blocks at this instant .
The acceleration of the centre of mass is given by aCM=FM=F2m
The position of the centre of mass at time t is x=12aCMt2=Ft24m
(b) Suppose the displacement of the first block is x1 and that the second is x2 . As ite centre of mass is at x , we should have
x=mx1+mx22morFt24m=x1+x(2)2
or x1+x2=Ft22m......(i)
The extension of the spring is x2−x1
Therefore , x2−x1=x0......(ii)
From (i) and (ii) ,
x1=12(Ft22m−x0)andx2=12(Ft22m+x0)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure. (a) Find the displacement of the centre of mass at time t. (b) If the extension of the spring is x0 at time t, find the displacement of the two blocks at this instant.

View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure. (a) Find the displacement of the centre of mass at time t. (b) If the extension of the spring is x0 at time t, find the displacement of the two blocks at this instant.

View Solution
Knowledge Check
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time t isAFt22mBFt23mCFt24mDFt2mTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant isA12(Ft22m+x0)B−12(Ft22m+x0)C12(Ft22m−x0)DFt22m+x0
Two block of equal mass m are connected by an unstretched spring and the sytem is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks puling it away from the other as shown in figure. a.Find the positon of the centre of mass at time t. b.If the extansion of the spring is x0 at time t find the displacement of the two blocks at this instant.
View SolutionTwo block of equal mass m are connected by an unstretched spring and the sytem is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks puling it away from the other as shown in figure. a.Find the positon of the centre of mass at time t. b.If the extansion of the spring is x0 at time t find the displacement of the two blocks at this instant.
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time t is
View Solutiontwo blocks of equal mass m are connected by an unstretched· spring and the system is kept at rest on a frictionless horizontal surface. A constant force Fis applied on one of the blocks pulling it away from the other as shown in Fig. ,4E.21(a)
(a) find tyhe position of CM at time t,
(b) if the extension of the spring is x0 at time t, find the displacement of the blocks at that instant.
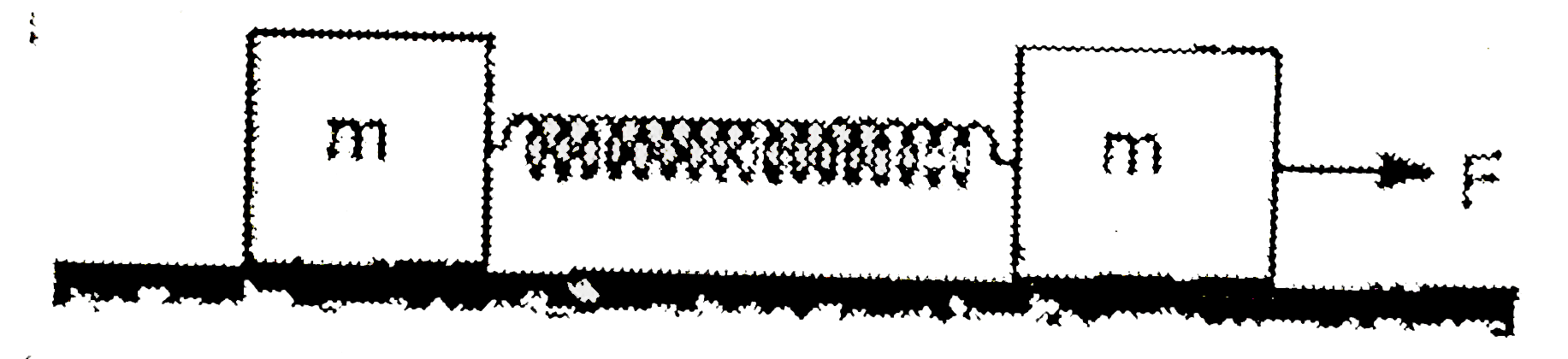
View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
 (a)Find accelaration of the mass center.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.
View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.
View Solution
