Three particles , each of mass m , are situated at the vertices of an equilateral triangle . Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC .

Perpendicular distance of A from AX = 0
Perpendicular distance f B from AX = L
Perpendicular distance of C from AX = L/2
Thus , the moment of inertia of the particle at A = 0 , of the partical at B=mL2 , and of the particle at C = m(L/2)2 . The moment f inertia of the three - partcicle system about AX is
0+mL2+m(L/2)2=5mL24
Note : The particles on the axis do not contribute to the moment of inertia
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View Solution
Knowledge Check
Three particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
 .A(3/4)ml2B2ml2C(5/4)ml2D(3/2)ml2
.A(3/4)ml2B2ml2C(5/4)ml2D(3/2)ml2Three particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
A3ma2Bma2Cma2/3D2/3ma2Three point masses, each of mass m, are situated at the three corners of an equilateral triangle of each side l. The moment of inertia of this system about one of the sides of the triangle will be -
Aml2B3ml2C34ml2D23ml2
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
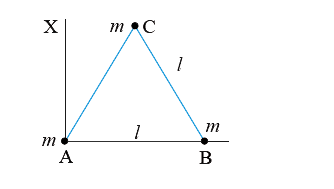
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).

The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionThree particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
 .
.
View SolutionThree light rods, each of length 2l, are joined together to form a triangle. Three particles A, B, C of masses m, 2m, 3m are fixed to the vertices of the triangle. Find the moment of inertia of the resulting body about
an axis through A perpendicular to the plane ABC,
View SolutionThree particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View Solution
