Find the moment of inertia of a circular disc or solid cylinder of radius R about the following axes .
(a) passing through the centre and perpendicular to the flat surface .
(b) at the rim and perpendicular to the flat surface
To find the moment of inertia of a circular disc (or solid cylinder) of radius R about the given axes, we will solve the problem step by step.
Part (a): Moment of Inertia about the Axis Passing through the Centre and Perpendicular to the Flat Surface
1. Understanding the Geometry:
- We have a circular disc of radius R and mass M.
- We need to find the moment of inertia about an axis that passes through the center and is perpendicular to the flat surface of the disc.
2. Consider an Elementary Ring:
- Take a thin ring of radius r and thickness dr at a distance r from the center.
- The mass of this ring, dm, can be expressed in terms of the area and mass per unit area.
3. Mass per Unit Area:
- The total area of the disc is A=πR2.
- The mass per unit area, σ, is given by:
σ=MπR2
4. Mass of the Ring:
- The area of the ring is dA=2πrdr.
- Therefore, the mass of the ring is:
dm=σ⋅dA=MπR2⋅2πrdr=2MR2rdr
5. Moment of Inertia of the Ring:
- The moment of inertia dI of this ring about the axis is given by:
dI=r2dm=r2(2MR2rdr)=2MR2r3dr
6. Integrate to Find Total Moment of Inertia:
- Now, integrate dI from r=0 to r=R:
I=∫R02MR2r3dr
- The integral evaluates to:
I=2MR2⋅(r44)R0=2MR2⋅R44=2MR24=MR22
7. Final Result for Part (a):
- The moment of inertia of the disc about the axis passing through the center and perpendicular to the flat surface is:
Ia=MR22
Part (b): Moment of Inertia about the Axis at the Rim and Perpendicular to the Flat Surface
1. Using the Parallel Axis Theorem:
- The parallel axis theorem states that:
IB=IA+Md2
- Where IA is the moment of inertia about the center (which we found in part (a)), and d is the distance from the center to the new axis.
2. Calculate the Distance:
- For the axis at the rim, the distance d is equal to the radius R.
3. Substituting Values:
- We already have IA=MR22 and d=R:
IB=MR22+MR2
- Simplifying this gives:
IB=MR22+2MR22=3MR22
4. Final Result for Part (b):
- The moment of inertia of the disc about the axis at the rim and perpendicular to the flat surface is:
Ib=3MR22
Summary of Results:
- (a) Moment of inertia about the center: Ia=MR22
- (b) Moment of inertia about the rim: Ib=3MR22
- We have a circular disc of radius R and mass M.
- We need to find the moment of inertia about an axis that passes through the center and is perpendicular to the flat surface of the disc.
- Take a thin ring of radius r and thickness dr at a distance r from the center.
- The mass of this ring, dm, can be expressed in terms of the area and mass per unit area.
- The total area of the disc is A=πR2.
- The mass per unit area, σ, is given by:
σ=MπR2
- The area of the ring is dA=2πrdr.
- Therefore, the mass of the ring is:
dm=σ⋅dA=MπR2⋅2πrdr=2MR2rdr
- The moment of inertia dI of this ring about the axis is given by:
dI=r2dm=r2(2MR2rdr)=2MR2r3dr
- Now, integrate dI from r=0 to r=R:
I=∫R02MR2r3dr
- The integral evaluates to:
I=2MR2⋅(r44)R0=2MR2⋅R44=2MR24=MR22
- The moment of inertia of the disc about the axis passing through the center and perpendicular to the flat surface is:
Ia=MR22
- The parallel axis theorem states that:
IB=IA+Md2
- Where IA is the moment of inertia about the center (which we found in part (a)), and d is the distance from the center to the new axis.
- For the axis at the rim, the distance d is equal to the radius R.
- We already have IA=MR22 and d=R:
IB=MR22+MR2
- Simplifying this gives:
IB=MR22+2MR22=3MR22
- The moment of inertia of the disc about the axis at the rim and perpendicular to the flat surface is:
Ib=3MR22
- (a) Moment of inertia about the center: Ia=MR22
- (b) Moment of inertia about the rim: Ib=3MR22
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 19videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 411videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)19videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis through the centre of the disc and perpendicular to its plane
View Solution
Knowledge Check
- Question 1 - Select One
Find the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
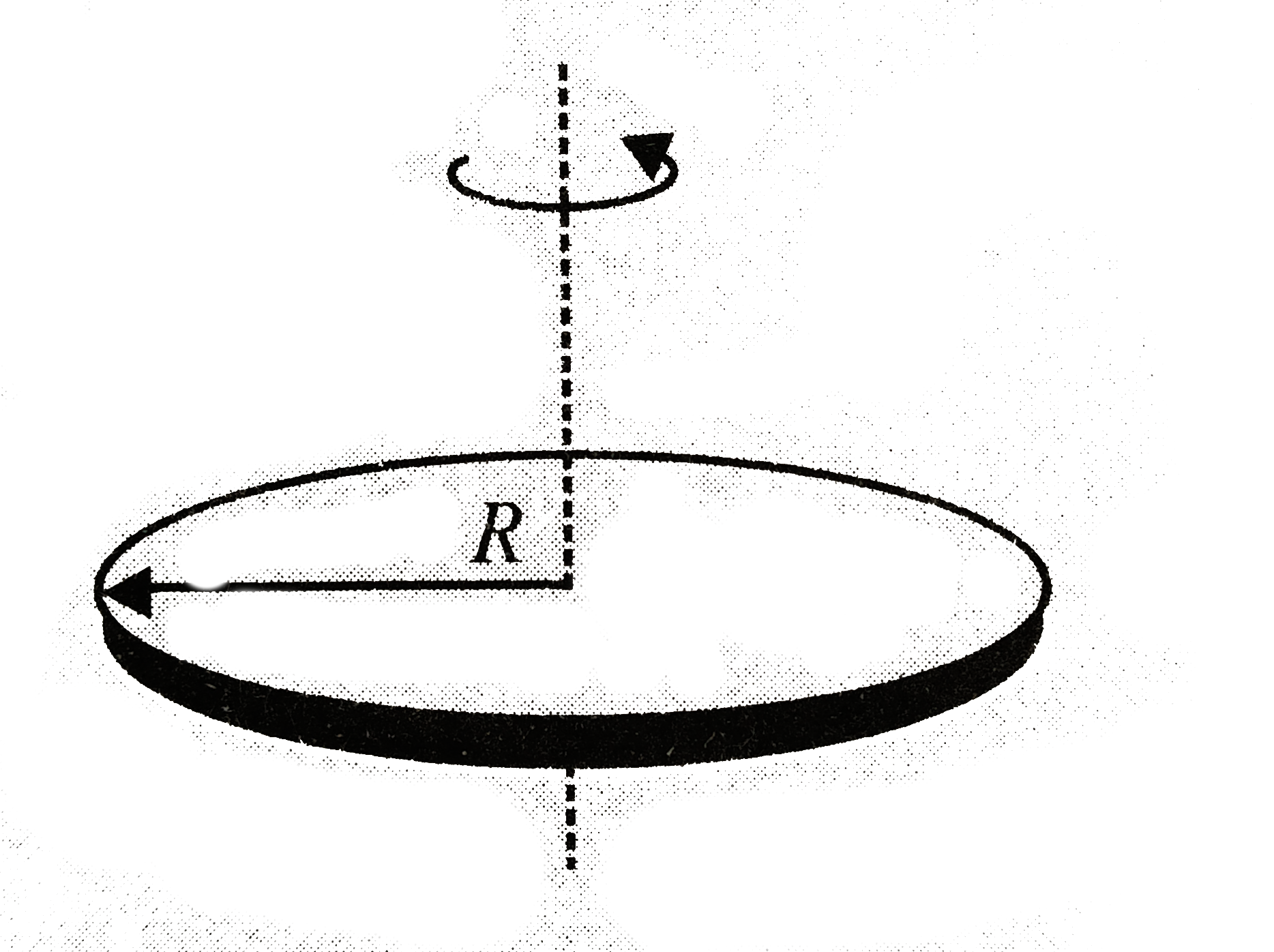 A12MR2B23MR2C32MR2DMR2
A12MR2B23MR2C32MR2DMR2 - Question 2 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2 - Question 3 - Select One
The moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212
Calculate the ration of radii of gyration of circular ring and a disc of the same radius about the axis passing through their centres and perpendicular to their planes.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionFind out the moment of inertia of the circular arcs shown, each having mass M, radius R and having uniform mass distribution about an axis passing through the centre and perpendicular to the plane ?
 View Solution
View SolutionMoment of inertia of a solid cylinder of length L and diameter D about an axis passing through its centre of gravity and perpendicular to its geometric axis is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View Solution

