A spool (cylinder) rotating about its axis and a mass 'm' tied it which falls as string is unwinded . Find the acceleration of the mass m and tension in the string

Considering F.B.D of m

For cylinder ,
T.R=τ=Iα=IaR⇒T=IaR2…..(2)
(##NARN∃TPHYXIP2C07SLV065_S02.png width=80%><br>Pu∈g(2)∈(1)a = g/((1+I/(mR^(2))))<br>Pu∈gI = (MR^(2))/2 (2mg)/(M+2m) T = (Mmg)/(M+2m)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
The block of mass m is at rest. Find the tension in the string A .

View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
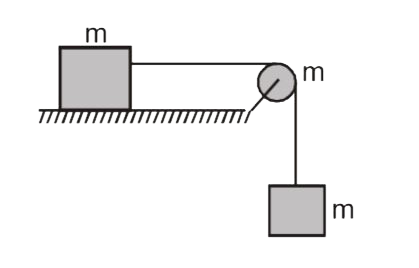
View Solution
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
Amgd3B−mgd3C23mgdD−23mgdA body of mass m is allowed to fall with the help of string with downward acceleration g/6 to distance x. The work done by the string is
Amgx6B−mgx6C5mgx6D−5mgx6
A block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.

View SolutionA spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.

View Solution
