A wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure . A string is wrapped over its rim and a block of mass m attached to the free end of the string . The system is released from rest . Find the speed of the block as it descends through a height h .

Let the speed of the block be v when it descends through a height h. The angular velocity of the wheel is v/r and its kinetic energy at the instant is I2Iv/r2 .Using the principle of conservation of energy . The gravitational potential energy lost by block and the wheel . Thus ,
mgh==12mv2+12Iv2r2
or v=[2mghm+I/r2]1/2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
A wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View SolutionA uniformly thick wheel with moment of inertia I and radius R is free to rotate about its centre of mass (see fig). A massless string is wrapped over its rim and two blocks of masses m1andm2(m1>m2) are attached to the ends of the string. The system is released from rest. The angular speed of the wheel when m1 descents by a distance h is :
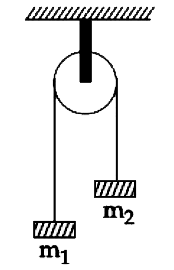
View SolutionA uniformaly thick wheel with moment of inertia I and radius R is free to rotate about its centre of mass (see fig). A massless string is wrapped over its rim and two blocks of masses m1andm2(m1>m2) are attached to the ends of the strung. The system is released from rest. The angular speed of the wheel when m1 descents by a distance h is :

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View Solution
