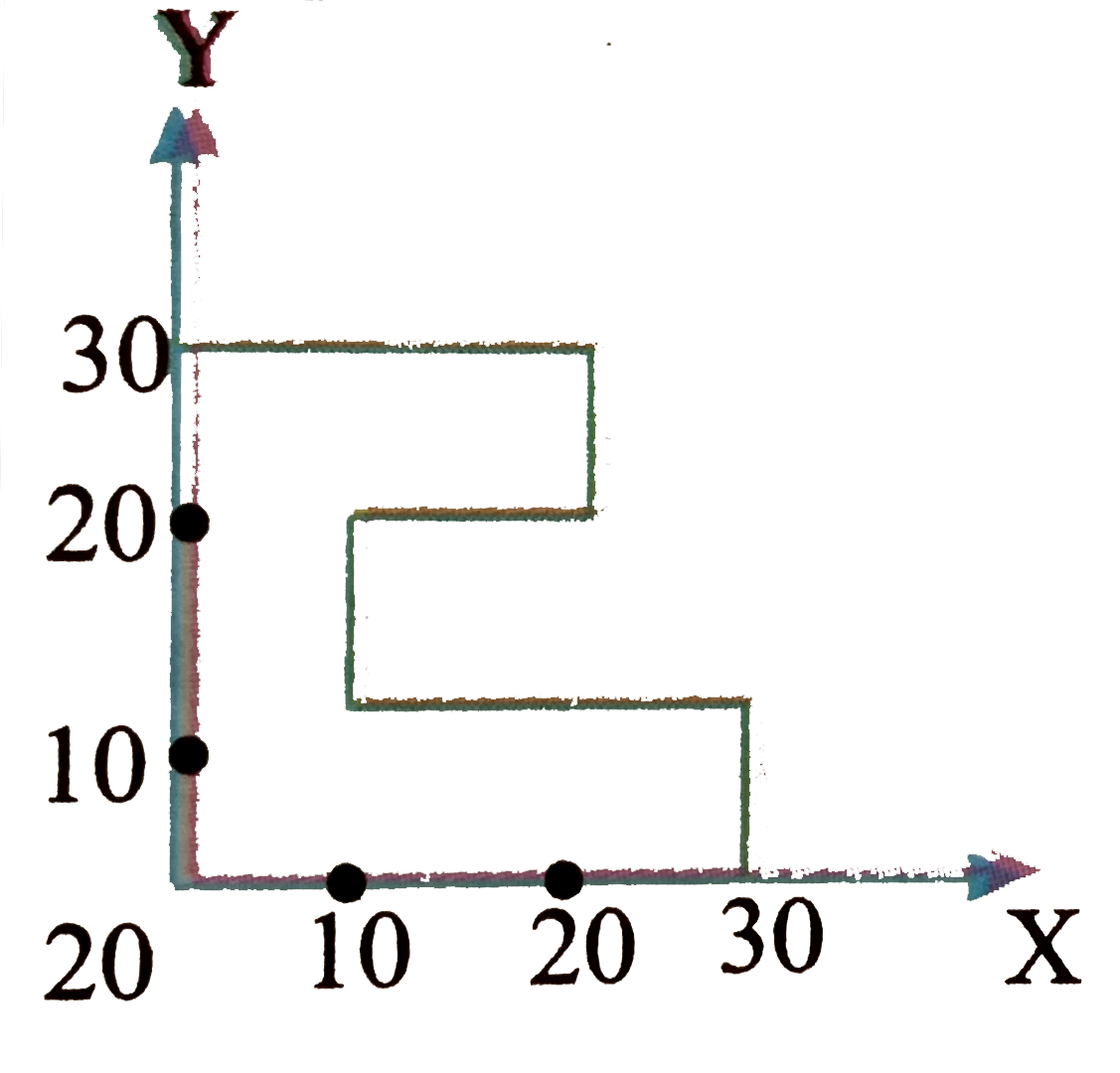
The coordinate of centre of mass of letter E which is cut from a uniform metal sheet are (take origin at bottom left corner and width of letter 2cm every where)

A

(2cm,4cm)

B

(2.4 cm , 5 cm)

C

(3 cm , 5cm)

D

(3.3cm,5cm)

Text Solution

Verified by Experts

The correct Answer is:B

$x_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3} + m_{4} x_{4}}{m_{1} + m_{2} + m_{3} + m_{4}}$
$y_{c m} = \frac{m_{1} y_{1} + m_{2} y_{2} + m_{3} y_{3} + m_{4} y_{4}}{m_{1} + m_{2} + m_{3} + m_{4}}$

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The co-ordinates of centre of mass of letter $E$ which is cut from a uniform metal sheet are (take origin at bottom left corner and width of letter $2 c m$ every where)

A $(2 c m, 4 c m)$
B $(2.4 c m, 5 c m)$
C $(3 c m, 5 c m)$
D $(3.3 c m, 4 c m)$
The centre of mass of the letter $F$ which is cut from a uniform metal sheet from point $A$ is

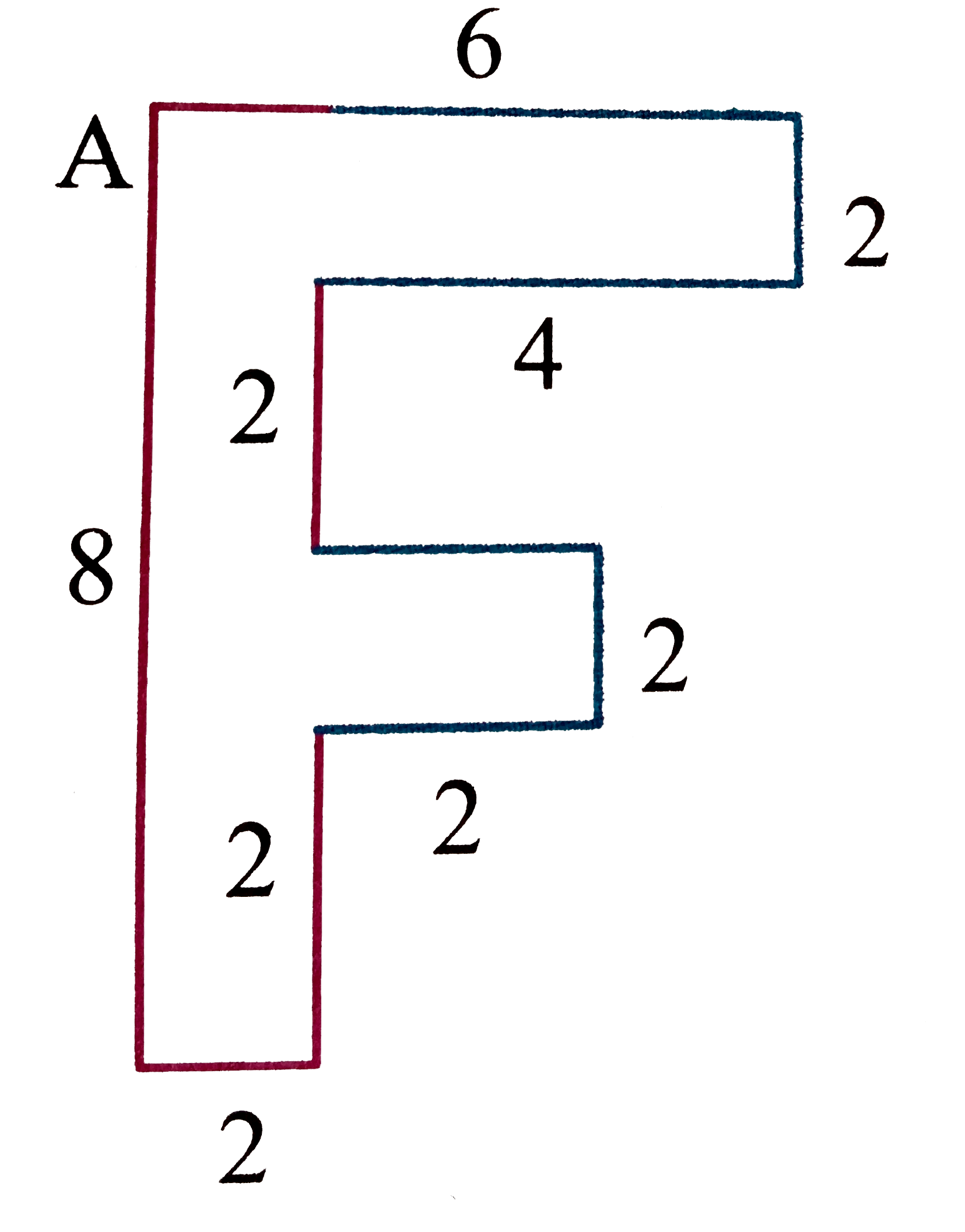A $15 / 7, 33 / 7$
B $15 / 7, 23 / 7$
C $22 / 7, 33 / 7$
D $33 / 7, 22 / 7$
Find the x coordinate of the centre of mass of the non - uniform rod of length L givne below. The origin is taken at the left end of the rod. The density of the rod as a function of its x- coordinates is $ρ = a x^{2} + b x + c$ , where a, b and c are constants.

A $\frac{2 a L^{2} + 3 b L^{2} + 6 c L}{2 (3 a L^{2} + 4 b L + 8 c)}$
B $\frac{4 a L^{3} + 3 b L^{2} + 2 c L}{2 (3 a L^{2} + 2 b L + c)}$
C $\frac{3 a L^{2} + 4 b L^{2} + 2 c L}{4 a L^{2} + 6 b L + 8 c}$
D $\frac{3 a L^{3} + 4 b L^{2} + 6 c L}{2 (2 a L^{2} + 3 b L + 6 c)}$

NARAYNA-SYSTEM OF PARTICLES AND ROTATIONAL MOTION -EXERCISE - II (H.W)

Home
Ask Doubt
Profile