Question

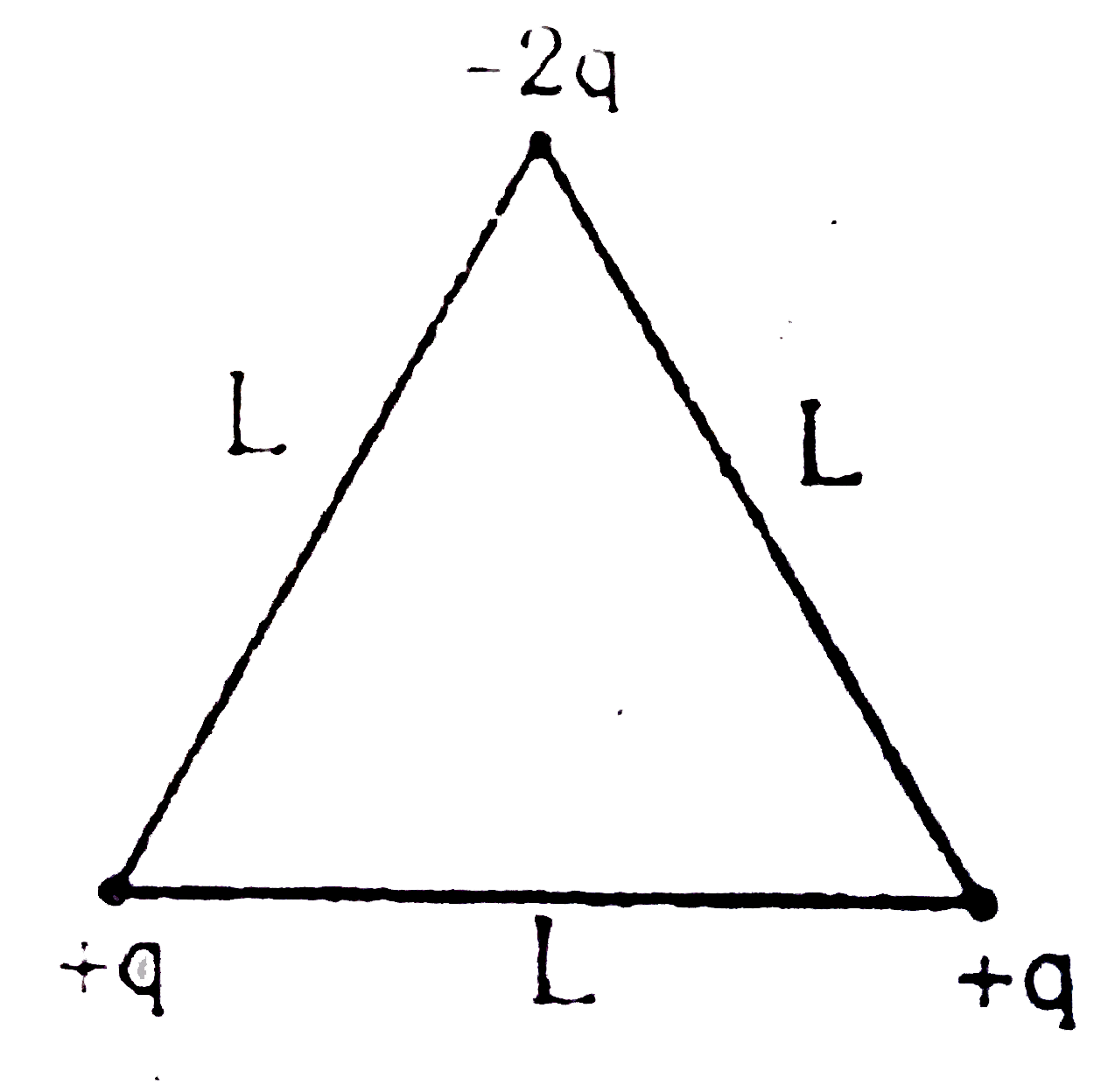
Three point charges q, q & - 2q placed, at the corners of equilateral triangle of side 'L ' Calculate work done by external force in moving all the charges far apart without acceleration

Options

A. `(1)/(4 pi epsilon_(0)) (3 q^(2))/(L)`
B. `-(1)/(4 pi epsilon_(0)) (3q^(2))/(L)`
C. `(1)/(4 pi epsilon_(0)) (5q^(2))/(L)`
D. `- (1)/(4 pi epsilon_(0)) (5 q^(2))/(L)`

Answer

A

Explanation

To solve the problem of calculating the work done by an external force in moving the three point charges $$q,q,$$ and $$-2q$$ placed at the corners of an equilateral triangle of side $$L$$ far apart without acceleration, we can follow these steps:

Step 1: Understand the System
We have three charges:
- Charge \( q \) at point A
- Charge \( q \) at point B
- Charge \( -2q \) at point C

These charges are positioned at the corners of an equilateral triangle with each side of length \( L \).

Step 2: Calculate the Initial Potential Energy of the System
The potential energy \( U \) of a system of point charges is given by the formula:

\( U = k \sum_{i < j} \frac{q_i q_j}{r_{ij}} \)

Where:
- \( k = \frac{1}{4 \pi \epsilon_0} \) is Coulomb's constant,
- \( r_{ij} \) is the distance between charges \( i \) and \( j \).

For our three charges, we will calculate the potential energy for each pair:

1. Between the two \( q \) charges:
\( U_{qq} = k \frac{q \cdot q}{L} = k \frac{q^2}{L} \)

2. Between one \( q \) charge and the \( -2q \) charge (two pairs):
\( U_{q(-2q)} = k \frac{q \cdot (-2q)}{L} = -2k \frac{q^2}{L} \)
Since there are two such pairs (one for each \( q \)):
\( U_{q(-2q)} \text{ (total)} = -2 \cdot 2k \frac{q^2}{L} = -4k \frac{q^2}{L} \)

Step 3: Sum the Potential Energies
Now, we sum all the potential energies to find the total initial potential energy \( U_{initial} \):

\( U_{initial} = U_{qq} + U_{q(-2q)} \text{ (total)} \)
\( U_{initial} = k \frac{q^2}{L} - 4k \frac{q^2}{L} = -3k \frac{q^2}{L} \)

Step 4: Calculate the Final Potential Energy
When all charges are moved far apart, the potential energy \( U_{final} \) of the system becomes zero because the distance between any two charges approaches infinity.

\( U_{final} = 0 \)

Step 5: Calculate the Work Done by External Force
The work done \( W \) by the external force in moving the charges is given by the change in potential energy:

\( W = U_{final} - U_{initial} \)
\( W = 0 - (-3k \frac{q^2}{L}) = 3k \frac{q^2}{L} \)

Step 6: Substitute the Value of \( k \)
Substituting \( k = \frac{1}{4 \pi \epsilon_0} \):

\( W = 3 \left(\frac{1}{4 \pi \epsilon_0}\right) \frac{q^2}{L} \)

Final Answer
Thus, the work done by the external force in moving all the charges far apart without acceleration is:

\( W = \frac{3q^2}{4 \pi \epsilon_0 L} \)