The diameters of the circumcirle of triangle ABC drawn from A,B and C meet BC, CA and AB, respectively, in L,M and N. Prove that 1AL+1BM+1CN=2R

Using sine rule in ΔOBL, we get
Rsin[π2+C−B]=OLsin(π2−A)
∴OL=RcosAcos(C−B)
⇒AL=R+RcosAcos(C−B)
=Rcos(C−B)+cosAcos(C−B)
=Rcos(C−B)−cos(B+C)cos(C−B)
=2RsinBsinCcos(C−B)
⇒1AL=cos(C−B)2RsinBsinC=2cos(C−B)sinA4RsinBsinCsinA=sin2B+sin2C4RsinBsinCsinA
⇒1AL+1BM+1CN
=2(sin2A+sin2B+sin2C)4RsinAsinBsinC
=2R
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.1
12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.2
8 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
Lex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that TX2=TB x TC
View SolutionLex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that TX2=TB x TC
View Solution
Knowledge Check
In a triangle ABC, BP is drawn perpendicular to BC to meet CA in P, such that CA = AP, then BPAB=
A2 sin AB2 sin BC2 sin CDnone of these
In the given figure L and M are the midpoints of AB and BC respectivcely
(i) If AB= BC prove that AL = MC
(ii) If BL = BM prove that AB=BC
View SolutionP,Q and R are, respectively, the mid-points of sides BC,CA and AB of a triangle ABC , PR and BQ meet at X.CR and PQ meet at Y . Prove that XY=14BC.
View SolutionIn triangle ABC , the internal bisector of ∠A∠Band∠C meet at point I . Prove that :
12(AB+BC+CA)<AI+BI+CI
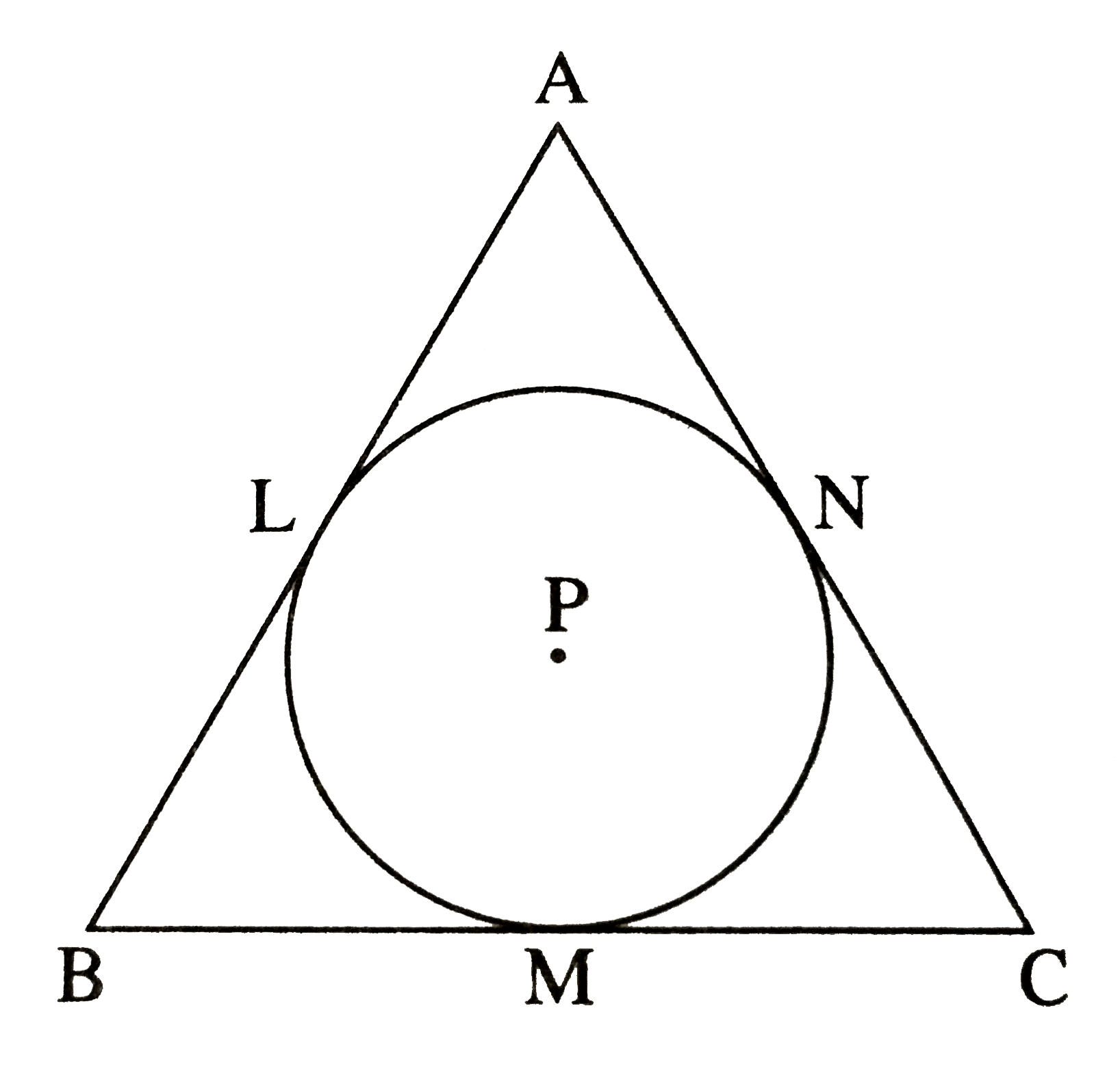
View SolutionA circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent
View SolutionABC is right angle triangle at C. Let BC = a, CA = b, AB = c and Let 'P' be the length of perpendicular from C to AB. prove that 1p2=1a2+1b2
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
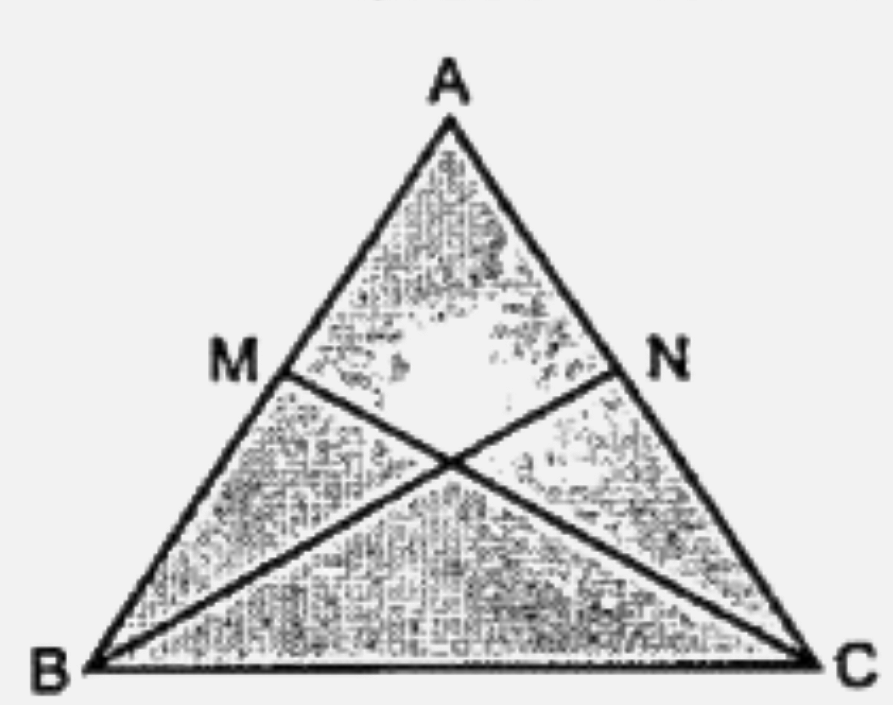
BN=CM
View Solution
