Lex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that TX2=TB x TC
Step by step video & image solution for Lex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that T X^2=T B x T C by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE∣∣AC and CF ∣∣ AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF)
View SolutionThe side BC of a triangle ABC is bisected at D;O is any point in AD.BOandCO produced meet ACandAB in EandF respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FE∣∣BC.
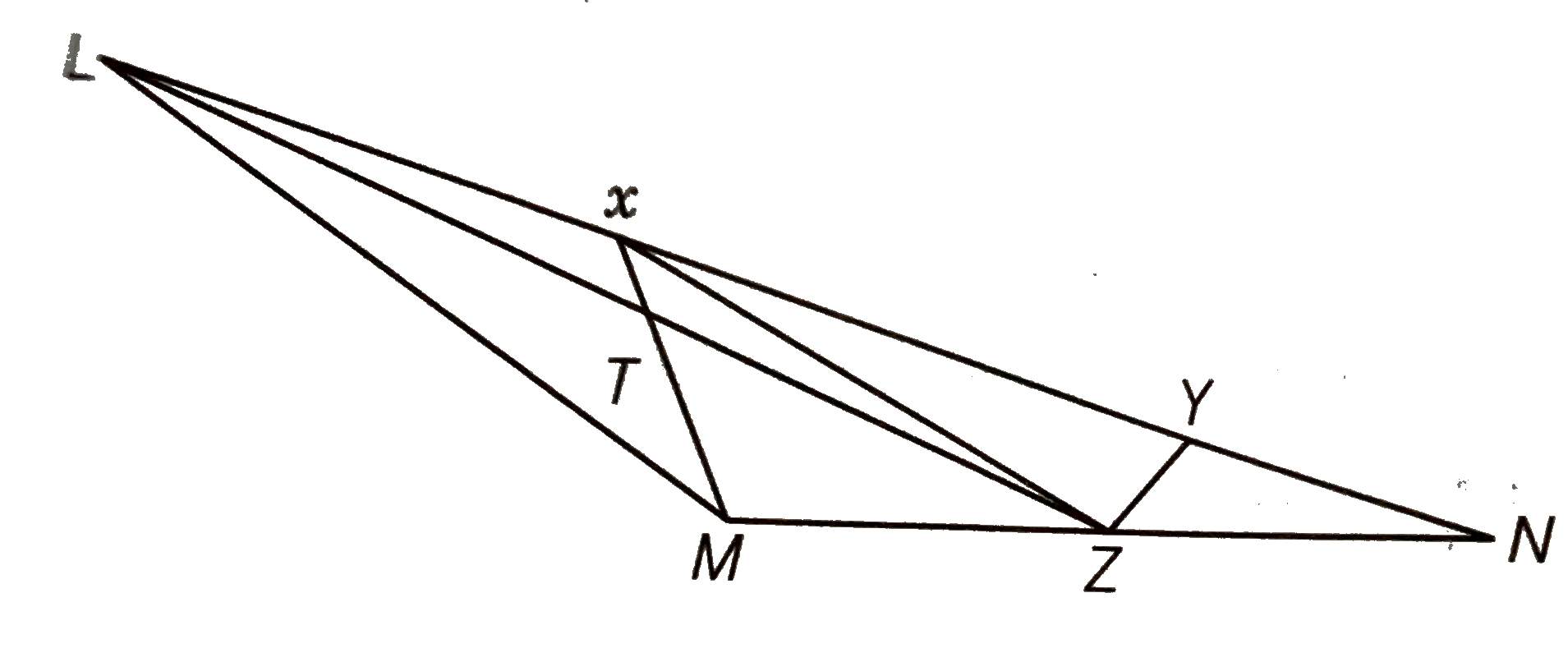
View SolutionX and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (see figure). Prove that ar(ΔLZY)=ar(MZYX).
View SolutionThe diameters of the circumcirle of triangle ABC drawn from A,B and C meet BC, CA and AB, respectively, in L,M and N. Prove that 1AL+1BM+1CN=2R
View SolutionIn triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and Glines are drawn parallel to AB which meet side BC at points M and N respectively.
Prove that : BM = MN = NC.
View SolutionO is any point in the plane of the triangle ABC,AO,BO and CO meet the sides BC,CA nd AB in D,E,F respectively show that ODAD+OEBE+OFCF=1.
View SolutionIn ΔABC the lines are drawn parallel to BC,CA and AB respectively through A,B and C intersecting at P, Q and R. Find the ration of perimeter of ΔPQR and ΔABC
View SolutionIn the adjoining figure, ΔPQR is formed by the sides PQ, QR and RP which are drawn parallel to sides AB,BC and CA respectively of ΔABC. Prove that
PQ+QR+RP=2(AB+BC+CA).

View Solution