ABCD एक चतुर्भुज है जिसमें AD=BC और ∠DAB=∠CBA है । सिद्ध कीजिए कि
BD=AC
Step by step video & image solution for ABCD एक चतुर्भुज है जिसमें AD=BC और /_DAB=/_CBA है । सिद्ध कीजिए कि BD=AC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - अभ्यास के लिए प्रश्न
4 Videos
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - दीर्घ उत्तरीय प्रश्न
1 Videos
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - अति लघु उत्तरीय प्रश्न
5 Videos
- चतुर्भुज BOOK - MBD HINDI-HARYANA BOARDCHAPTER - चतुर्भुज EXERCISE - बहुविकल्पी प्रश्न
6 Videos
- दो चरों वाले रैखिक समीकरण BOOK - MBD HINDI-HARYANA BOARDCHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - अभ्यास के लिए प्रश्न
11 Videos
Similar Questions
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है जिसमें AB=AC है। दर्शाइए कि
(i) AD रेखाखण्ड BC को समद्विभाजित करता है। (ii) AD कोण A को समद्विभाजित करता है।
View Solutionकिसी Δ की समान भुजाओं के सम्मुख कोण समान होते हैं।
दिया है: ΔABC में AB=AC
सिद्ध करना है ∠C=∠B
View Solutionत्रिभुजों का SAS सर्वांगसमता नियम क्या है?
View Solutionएक समांतर चतुर्भुज के कोणों के समद्विभाजक क्या बनाते हैं ?
View Solution−2x+3y=6 रैखिक समीकरणों को ax + by + c = 0 के रूप में व्यक्त कीजिए और प्रत्येक स्थिति में a, b और c के मान बताइए ?
View SolutionABCD is a quadrilateral in which AD = BC and /_DAB = /_CBA Prove that (i) DeltaABD ~= DeltaBAC (ii) BD = AC (iii) /_ ABD = /_BAC
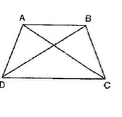
View SolutionIn the figure AD = BC and BD = CA. Prove that ∠ADB=∠BCA and ∠DAB=∠CBA
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
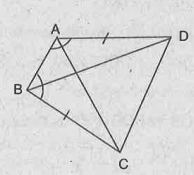
View SolutionABCD చతుర్భుజంలో AD=BC మరియు ∠DAB=∠CBA అయిన ΔABD≅ΔBAC
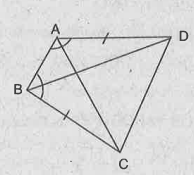
View SolutionABCD చతుర్భుజంలో AD=BC మరియు ∠DAB=∠CBA అయిన BD=AC
View Solution
