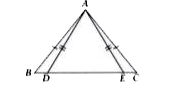
In the figure AD = BC and BD = CA. Prove that ∠ADB=∠BCA and ∠DAB=∠CBA

Video Solution

Answer

Step by step video & image solution for In the figure AD = BC and BD = CA. Prove that ∠ADB=∠BCA and ∠DAB=∠CBA by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS CONGRUENCE OF TRIANGLES

Topper's Solved these Questions

BOOK - RD SHARMACHAPTER - CIRCLE EXERCISE - All Questions
306videos
CIRCLE
BOOK - RD SHARMACHAPTER - CONSTRUCTION EXERCISE - All Questions
29videos
CONSTRUCTION

Knowledge Check

Question 1 - Select One
In the given figure $A D = B C, A C = B D$ . Then $Δ P A B$ is

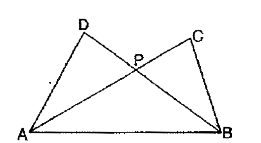Aequilateral
Bright angled
Cscalene
Disosceles

In the adjoining figure, AB = AC and BD = DC. Prove that $△ A D B = △ A D C$ and hence show that
(i) $∠ A D B = ∠ A D C = 90^{\circ}$ , (ii) $∠ B A D = ∠ C A D$ .

View Solution
In Figure $A B D C a n d A D B C .$ Prove that $∠ D A B = ∠ D C B$

View Solution
In the figure AD = BC and BD = CA. Prove that ∠ADB=∠BCA and ∠DAB=∠CBA

View Solution
In the given figure of AD = CB then prove that AC = BD
View Solution
In the adjoining figure, $A B = A C$ and $B D = D C$ Prove that $Δ A D B \equiv Δ A D C$ and hence show that (i) $∠ A D B \equiv ∠ A D C = 90^{\circ}$ , (ii) $∠ B A D = ∠ C A D$
View Solution
In the figure, AD is the bisector of angle BAC. Prove that AB>BD.
View Solution
In theadjoining figure, $∠ D A B = ∠ A B C$ and $A D = B C$ prove that $B D = A C$ .

View Solution

RD SHARMA-CONGRUENT TRIANGLE -All Questions

A point O is taken inside an equilateral four sided figure A B C D suc...
03:32
In Figure, two sides A B\ a n d\ B C and the median A D\ of A B C ar...
04:53
In the figure AD = BC and BD = CA. Prove that ∠ADB=∠BCA and ∠DAB=∠CBA
01:56
In figure, AB = AC, D is the point in the interior of ABC such that DB...
01:51
In Figure, it is given that A B=C D\ a n d\ A D=B Cdot Prove that A...
02:27
In A P Q R , if P Q=P Q\ a n d\ L ,\ M\ a n d\ N are the mid-points o...
02:55
A D ,\ B E\ a n d\ C F , the altitudes of A B C are equal. Prove that...
04:26
In Figure, it is given that L M=M N ,\ Q M=M R ,\ M L\ |P Q\ a n d\ ...
02:14
If A B C is an isosceles triangle such that A B=A C and A D is an alti...
02:03
P is a point equidistant from two lines l and m intersecting at poin...
03:54
A B C is a triangle and D is the mid-point of B C . The perpendiculars...
02:32
A B C is a triangle is which B E and C F are, respectively, the perpen...
02:12
In perpendiculars from any point within an angle on its arms are con...
01:33
In Figure, A D\ |C D\ and C B\ |c ddot If A Q=B P\ a n d\ D P=C Q , p...
02:28
A B C D is a square, X\ a n d\ Y are points on sides A D\ a n d\ B C r...
01:58
Which of the following statements are true (T) and which are false (...
04:45
Fill the blanks in the following so that each of the following stateme...
03:31
In a A B C ,\ if /A=45^0\ a n d\ /B=70^0dot Determine the shortest ...
01:46
In a A B C , if /A=50^0\ a n d\ /B=60^0 , determine the shortest a...
01:49
In Figure, P Q > P RdotQ S\ a n d\ R S are the bisectors of L Q and /R...
01:30

Home
Ask Doubt
Profile

In the figure AD = BC and BD = CA. Prove that ∠ADB=∠BCA and ∠DAB=∠CBA

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the given figure AD=BC,AC=BD. Then ΔPAB is

RD SHARMA-CONGRUENT TRIANGLE -All Questions

In the given figure $A D = B C, A C = B D$ . Then $Δ P A B$ is