Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
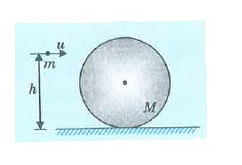
Angular velocity of the sphere just after the collision is
5mu2MR
5mu(h−R)2MR2
2mu(h−R)5MR2
2Mu(h−R)2mR2
The correct Answer is:B
We can apply conservation of angular momentum about centre of sphere just before and just after the collision.
L1=L2
mu(h−R)=[25MR2+mR2]ω
ω=mu(h−R)25MR2+mR2=mu(h−R)(25M+m)R2
Since M>>m so we can neglect m in the denominator in comparison to M.
ω≈(5mu)(h−R))2MR2
Hence option (b) is corrrect.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
View SolutionA hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
View Solution
Knowledge Check
Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.A5R7B3R5C3R7D7R5Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

What will be the approximate velocity of combined system after the collision?AmuMBmu2MC2muMDzero
A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionA uniform sphere of mass m and radius R is placed on a rough horizontal surface. The sphere is struck horizontally at a heighth from the floor. Match the following:

View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
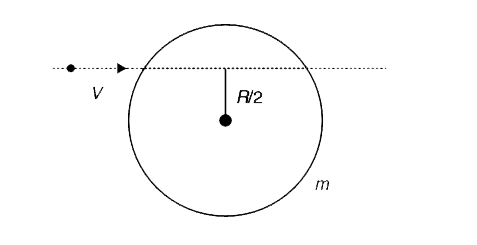
View Solution
