State of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
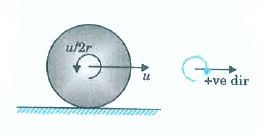
At what time sphere starts pure rolling?
2u7μg
3u5μg
3u7μg
5u7μg
The correct Answer is:C
We can continue with the solution discussed so far in previous part. Let us first write linear and angular speed of the sphere at some instant of time t.
u=u+at+⇒u=v−μgt ...(iii)
ω=ω0+αt⇒ω=−u2r+5μg2rt ...(iv)
For pure rolling we have v rohence we can write the following:
u=rω⇒u−μg=−u2+5μg2t
⇒μgt=3u7 ...(v)
Hence time to start pure rolling can be written from equation (v)
t=3u7μg
Hence option (c) is correct.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
Explore 10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
Explore 3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
Explore 48 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A hollow sphere of radius r is rotating about a horizontal axis at some angular speed ω0. It is gently lowered to ground and the coefficient of friction between sphere and the ground is μ.How far does the sphere move before it starts pure rolling?
View Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
View Solution
Knowledge Check
State of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here r is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assuming coefficient of friction between sphere and the surface. Mass of sphere is m.
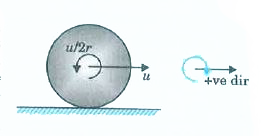
At what time sphere stops rotating for a moment?Au5μgB2u5μgC3u7μgD2u7μgState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
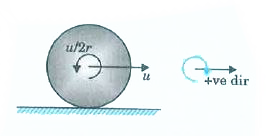
What will be the speed of sphere when it starts pure rolling?A4u7B3u7C2u7Du7State of the sphere at some instant of time is shown in figure. Surface below the sphere is rough. At the given instant, speed of the centre of the sphere is u and angular velocity about the centre is u/2r. Select correct statement (s)
ADirection of friction on the sphere is towards leftBDirection of friction on the sphere is towards rightCAngular momentum about point o remains conservedDAngular momentum about point B remains conserved
A solid sphere is set into motion on a rough horizontal surfce with a linar speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown infigure . Find the linear speed of the sphere a. where it stops rotating and b. when slipping finally ceases sand pure rolling starts.

View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
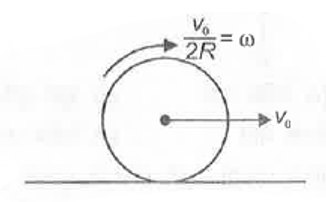
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
View SolutionA sphere A moving with a speed u and rotating with an angular velocity ω, makes a head-on elastic collision with an identical stationary sphere B. There is no friction between the surfaces of a and B. Disregard gravity.
View Solution
