A cubical block of wood of specific gravity 0.5 and chunk of concrete of specific gravity 2.5 are fastened together. the ratio of mass of wood to the mass of concrete which makes the combination to float with entire volume of the combination submerged in water is
m=Mass of solid sphere
p=Density of solid sphere
m.=Mass of cavity
p.=Density of cavity
R=Radius of sphere
r=Radius of cavity
Masss of solid sphere =43π(R3−r3)p=m
Mass of cavity =43πr3p.=m.
mm,=43πR3−r3p43πr3p.
=R3−r3r3pp.......(i)
As the sphere of volume V and radius R is submerged under water.
Therefore, using principle of floatation we can write
Weight of water displaced= Weight of solid sphere +Weight of sawdust
vpwg=mg+m.g
pw=density of water
vpw=43π(R3−r3)p+43πr3p.
43πR3pw=43π(R3−r3)p+43πr3p.
R3=R3−r3ppw+r3p.pw
As ppw= relative density of solid sphere =σ
p.pw =relative density of sawdust =σ.
R3=(R3−r3)σ+r3σ.
R3−R3σ=r3σ.−r3σ
R3(1−σ)=r3(σ.−σ)
R3r3=σ.−σ1−σ
R3r3−1=σ.−σ1−σ−1
R3−r3r3=σ.−σ−1+σ1−σ=σ.−11−σ
From (i) mm.=R3−r3r3(pp.)
As pp.=σσ.
mm.=(σ.−11−σ)(σσ.)
As σ=4.8,σ.=0.6
mm.=(0.6−11−4.8)(4.80.6)
=−0.43.8×4.80.6=0.8
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Textbook Exercises)
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Additional Exercises)
11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A block of wood weighing 71.2N and of specific gravity 0.75 is tied by a string to the bottom of a tank of water in order to have the block totally immersed, What is the tension in the string?
View SolutionA cubical block of wood weighing 200g has a lead piece fastened underneath. Find the mass of the lead pieces which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
(b) Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
View Solution
Knowledge Check
wood with specific gravity of less than 0.2 is
AbombaxBpopulusCochromaDOlea.A block B of specific gravity 2 and another block C of specific gravity 0.5 .Both are joined together and they are floating water such that they are completely dipped inside water , the ratio of the masses of the blocks B and C is
A2:1B3:2C5:3D2:3A small block of wood, of specific gravity 0.4 is submerged in water at a depth of 2.9 m. If the block is released from rest. Then choose the correct alternative(s).
AAcceleration of block towards the surce is 14.7m/s2BVelocity of block after 3 s is 29.4m/sCTime taken by the block to reach the surface is 0.63 sDTime taken by the block to reach the surface is 2.74 s
The specific gravity (or relative density) of gold is 19. Find the mass of a gold body that displaces 25cm3 of water when immersed in it.
View SolutionA cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just alow the block of float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
View SolutionA cube made of wood having specific gravity 0.4 and side length a is floated in a large tank full of water.
 Which action would change the depth to which block is submerged?
Which action would change the depth to which block is submerged?
View SolutionFor a pure liquid (Specific gravity 2) having molar mass 50gm/mol. Ratio of molarity to molality is:
View Solution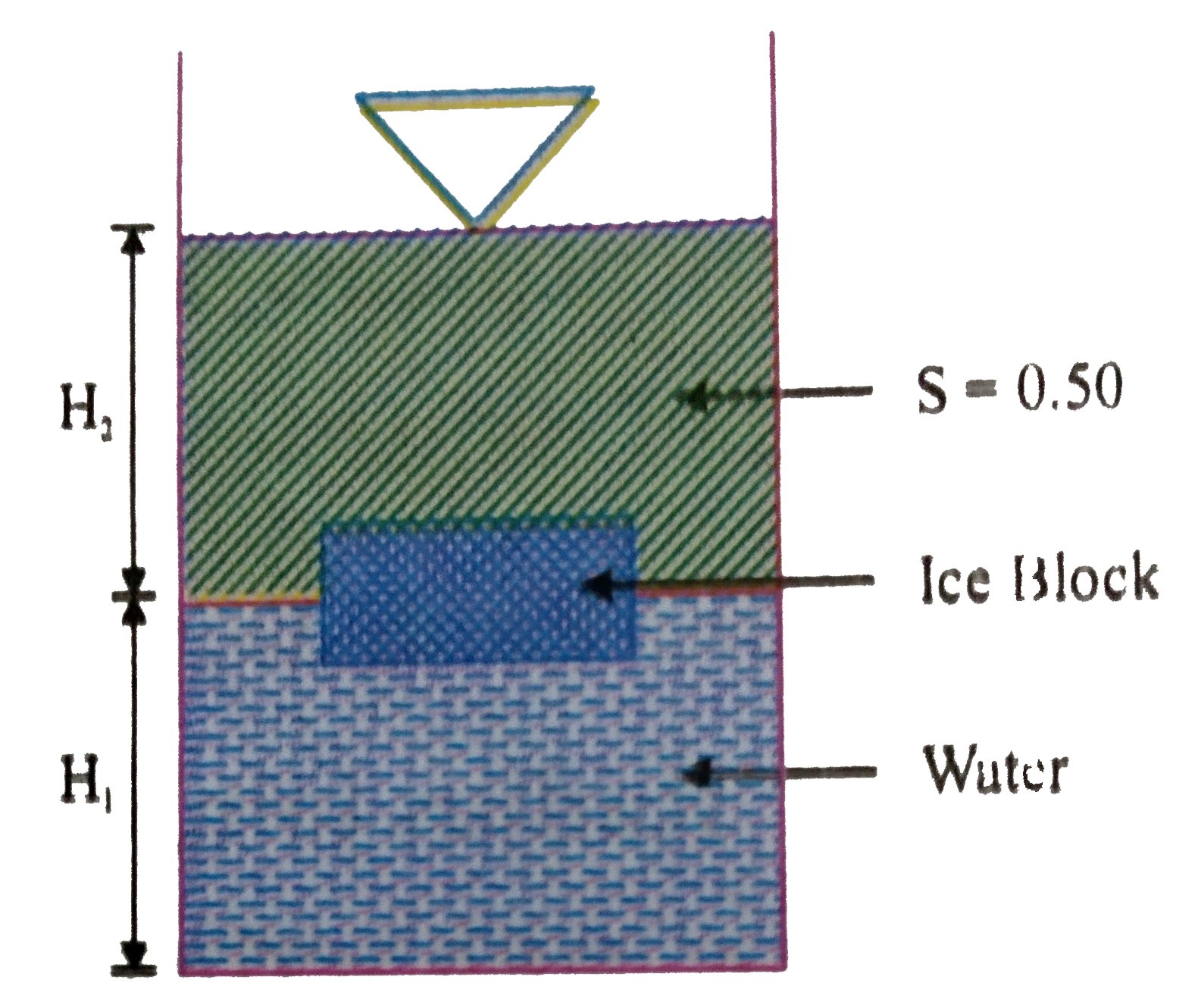
A block of ice (specified gravity Si−=0.90) is floating in a container having two immiscible liquids (one of specific gravity S=0.50 and other is water) as shown in the figure. (H,H2 are height of water other liquid columns respectively). Now the ice block melts completely,then
View Solution