A square loop of edge a, and a long straight conductor carrying current I are placed coplanar as shown in figure. Self-inductance and resistance of the square loop are L and R, respectively.

Find the electric charge that flows in square loop when it is turned through 180∘ about an axis PQ as shown in figure.
If induced emf in the square loop is E and current flowing through it is i, then we can write the following equation:
E−iR−Ldidt=0
⇒R=Edt−Ldi
emf induced E, can be written as dϕ/dt , and hence above equation can be written as follows:
⇒R=−dϕdtdt−Ldi
⇒R=−dϕ−Ldi
⇒R∫=−∫dϕ−L∫di
⇒Rq=(ϕ1−ϕ2)−L(if−ii)

Since initial and final currents are both equal to zero (ii=0,if=0) and hence we can rewrite above equation as follows:
⇒Rq=(ϕ1−ϕ2)
⇒Rq=(ϕ1−ϕ2)
⇒q=(ϕ1−ϕ2R) ...(i)
To calculate magnetic flux linked with the loop let us select a segment of width dx at a distance x from the straight conductor. Area of this segment is a dx and magnetic field intensity due to current in wire can be written as follows:
B=μ0I2πx
We need to calculate magnetic flux only in the initial state and final state and both the states magnetic field is perpendicular to the plane of the square. Hence flux linked with the segment can be written as follows:
dϕ=Badx=μ0I2πxadx
⇒dϕ=μ0Ia2πdxx ...(ii)
In the first case lower limit of x is b and upper limit of x is a +b, hence ϕ1 can be written as follows:
ϕ1=μ0Ia2π∫a+bbdxx
ϕ1=μ0Ia2πIna+bb ...(iii)
Similarly, we can find ϕ2=μ0Ia2πIn2a+ba+b ...(iv)
Substituting equations (iii) and (iv) in equation (i) we get q.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Very Short Answer Questions Carrying I mark)
44 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Additional Questions (Carrying I mark))
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Short answer type questions)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A square wire frame ( initially current is zero) with side a and a straight conductor carrying a constant current I are located in the same plane (figure). The inductance and the resistance of the frame are equal to L and R respectively. The frame was turned through 180∘ about the axis OO' separated from the current - carrying conductor by a distance b=2a. The total electric charge having flown through the frame if i=0 at t=0 in the loop is equal to μ0aI2πRlnx. Find the value of x.
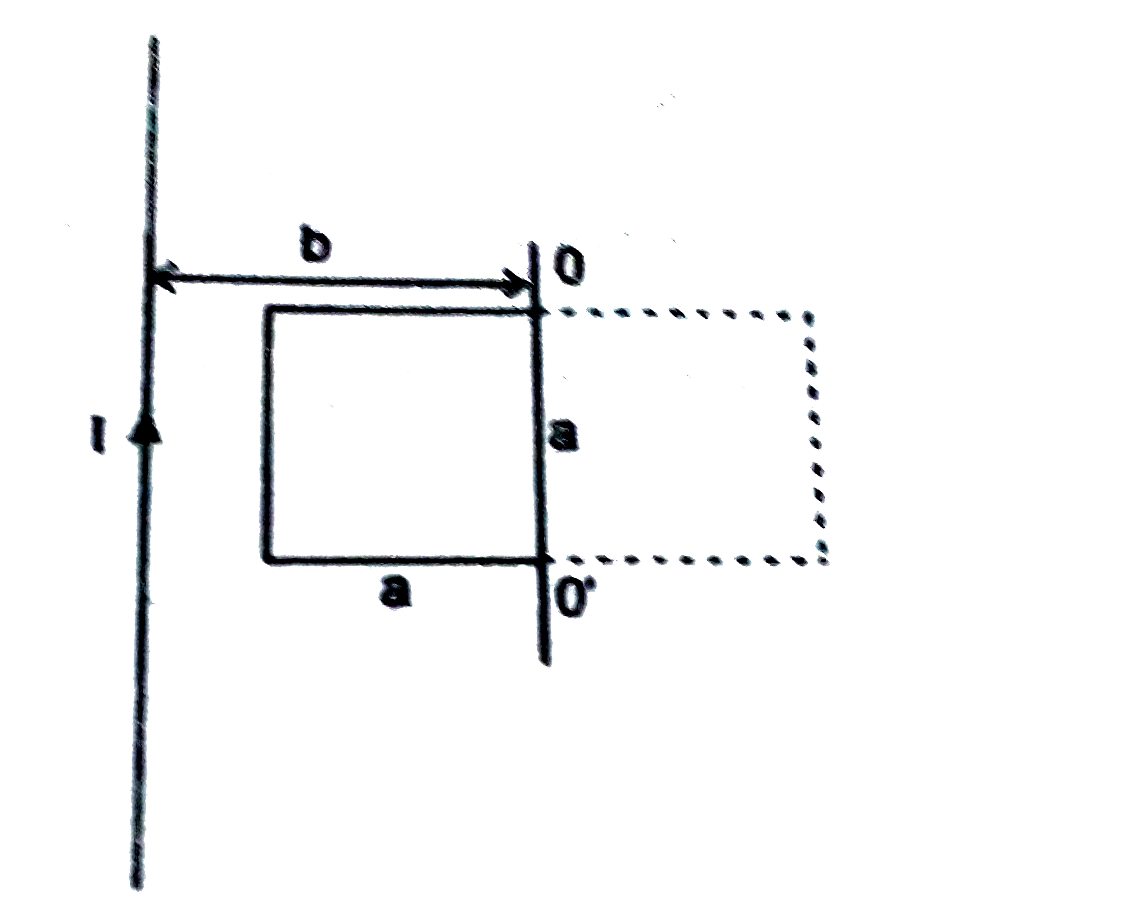
View SolutionA square wire frame ( initially current is zero) with side a and a straight conductor carrying a constant current I are located in the same plane (figure). The inductance and the resistance of the frame are equal to L and R respectively. The frame was turned through 180∘ about the axis OO' separated from the current - carrying conductor by a distance b=2a. The total electric charge having flown through the frame if i=0 at t=0 in the loop is equal to μ0aI2πRlnx. Find the value of x.

View Solution
Knowledge Check
A square loop of side as and a straight long wire are placed in the same plane as shown in figure. The loop has a resistance R and inductance L. The frame is turned through 180∘ about the axis OO′. What is the electric charge that flows through the loop?
 Aμ0Ia2πRln(2a+bb)Bμ0Ia2πRln(bb2−a2)Cμ0Ia2πRln(a+2bb)DNoneof these
Aμ0Ia2πRln(2a+bb)Bμ0Ia2πRln(bb2−a2)Cμ0Ia2πRln(a+2bb)DNoneof theseA rectangular loop carryinig current I is located near an infinite long straight conductor carrying current I as shown in the figure. The loop,
 Aremain stationaryBis attracted towards the wireCis repelled away from the wireDwill rotate about an axis parallel to the wire
Aremain stationaryBis attracted towards the wireCis repelled away from the wireDwill rotate about an axis parallel to the wire
A square loop of side as and a straight long wire are placed in the same plane as shown in figure. The loop has a resistance R and inductance L. The frame is turned through 180∘ about the axis OO′. What is the electric charge that flows through the loop?

View SolutionA square loop is placed near a long straight current carrying wire as shown. Match the following table.
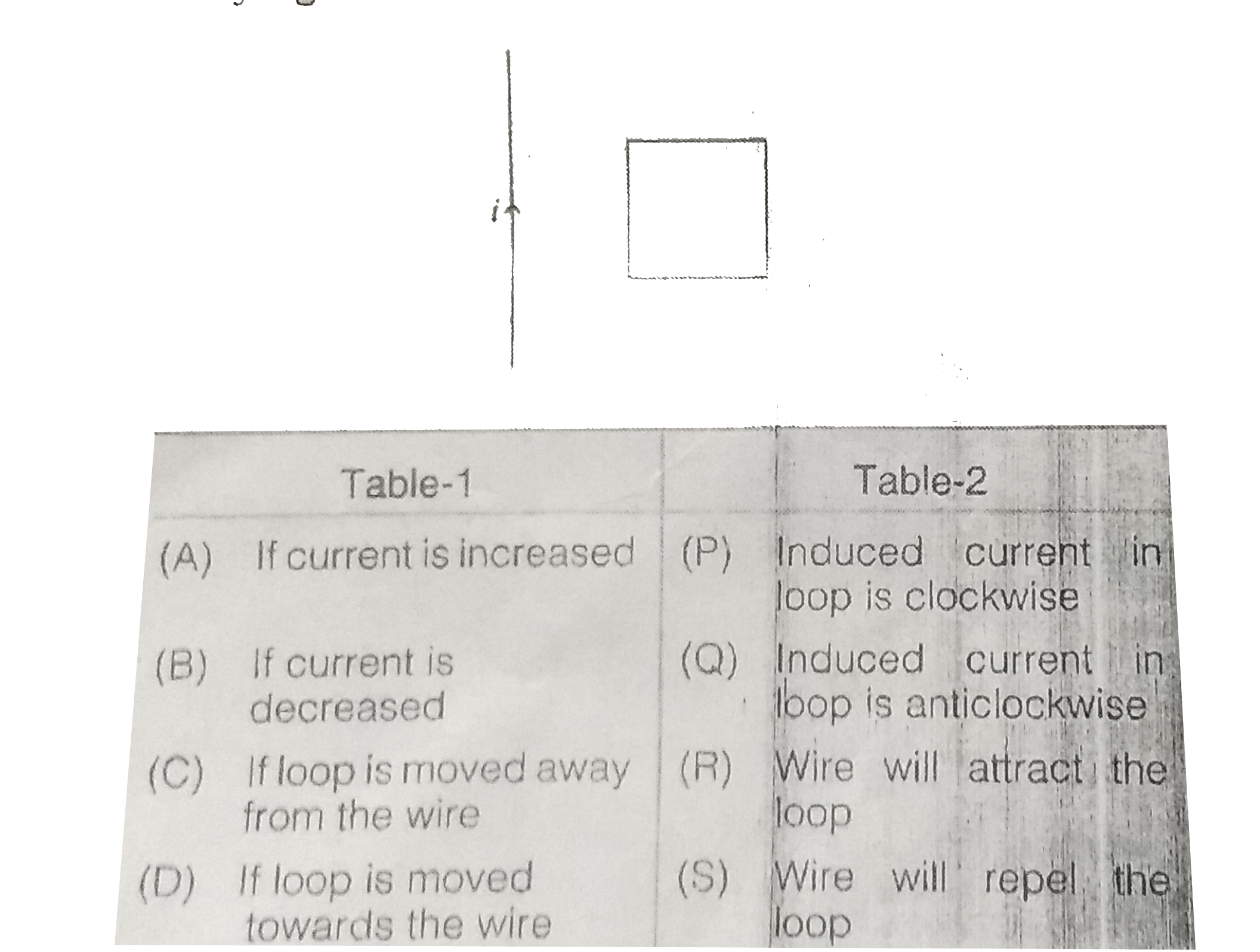
View SolutionA square loop is placed near a long straight current carrying wire as shown. Match the following table.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View Solution
