Inductors of self-inductances L1 and L2 having resistances R1 and R2 are connected to a circuit along with two other resistors R3 and R4 as shown in figure. Find the condition so that no current flows through galvanometer.

Let i1 and i2 be the electric currents flowing in the branches ACB and ADB as shown in figure.
No current is flowing through the galvanometer hence VC=VD, hence we can say that potential difference between A and C is same as A and D.
VAC=VAD
⇒L1di1dt+i2R1=L2di2dt+i2R2 ...(i)
Similarly, we can say that potential difference between C and B is the same as D and B. VCB=VDB
⇒i1R3=i2R4 ...(ii)
From equation (ii) we can substitute i1=i2R4R3 in equation (i) to get the following:
L1R4R3di2dt+i2R1R4R3=L2di2dt+i2R2
⇒L1R4R3di2dt−L2di2dt=i2R2−i2R1R4R3
⇒(L1R4R3−L2)di2dt=i2(R2−R1R4R3) ...(iii)
Now let us analyse equation (iii) for boundary conditions.
At t = 0, we have i2=0, hence right-hand side of equation (iii) becomes zero. Hence the left-hand side must also be zero at t = 0, but we know that di2/dt is not equal to zero at t = 0, hence (L1R4R3−L2) must be zero on the left-hand side. So we can write the following equation:
L1L2=R3R4 ...(iv)
At t=∞ , we know that i2 becomes constant and hence di2/dt=0 So the left-hand side of equation (iii) becomes zero at t=∞. Right-hand side of equation (iii) must also be zero at t=∞ Since i2, is non-zero and hence, the other term (R2−R1R4R3) must be zero, so we can write the following equation:
R1R2=R3R4 ...(v)
On combining equations (iv) and (v) we get the following condition for no current through galvanometer:
L1L2=R1R2=R3R4
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Very Short Answer Questions Carrying I mark)
44 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Additional Questions (Carrying I mark))
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Short answer type questions)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Two inductors of self inductances L1andL2 and of resistances R1andR2 (not shown) respectively are conneted in the circuit as shown. At the instant t = 0, key k is closed. Obtain an expression for which the galvanometer will show zero deflection at all times after the key is closed.
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View Solution
Knowledge Check
Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
AR>R1+R2BR1<R<R2CR2<R<(R1+R2)DR<R1Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
AR>R1+R2BR1<R<R2CR2<R<(R1+R2)DR<R1
Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionFind the currents going through the three resistors R1,R2 and R3 in the circuit of figure.

View SolutionTwo cells of emf E1 and E2 are connected to two resistors R1andR2 as shown. If E2 is short circuited then current through R1andR2 are

View SolutionFind the currents going through the three resistors R_(v),R_(2)andR_(3) in the circuit of figure.

View SolutionTwo resistance R1 and R2 are joined as shown in figure to two batteries of emf E1 and E2. If E2 is short circuited, what is the current through R1 ?

View SolutionTwo ideal batteries of emf V1andV2 and these resistances R1,R2andR3 are connected as shown in the figure . The current in resistance R2 would be zero if
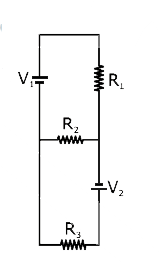
View Solution
