There is small circular coil which is suspended through a wire of length l to a rigid support. Initially, thread is kept vertical and uniform magnetic field B is applied perpendicular to the plane of circular coil. Coil is slightly displaced through an angle θ0 and released in such a manner that while oscillating plane of the coil always remains along the thread and it does not rotate about it. Calculate emf induced in the coil as a function of time assuming t = 0 at some instant when thread is vertical.
Initially when thread is vertical then angle between magnetic field and area vector of coil is zero. When thread makes an angle θ with the vertical then angle between magnetic field and area vector of coil also becomes θ. Hence magnetic flux linked with the coil can be written as follows:
ϕ=BAcosθ
We can apply Faraday.s law to get emf induced in the coil as follows:
ε=−dϕdt=BAsinθdϕdt
Here angle θ is given to be very small. Hence we use sinθ≈θ to rewrite the above relation as follows:
ε=BAθdthηdt
We know that coil performs SHM. And the angle the thread makes with the vertical can be written as follows:
θ=θ0sinωt
where ω=√gl
On differentiating equation (ii) we get the following:
dthηdt=θ0ωcosωt ...(iii)
Substituting from equation (ii) and (iii) in equation (i) we get the following:
ε=BA(θ0sinωt)(θ0ωcosωt)
⇒ε=BAωθ20sinωtcosωt
⇒ε=12BAωθ20sin2ωt
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Very Short Answer Questions Carrying I mark)
44 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Additional Questions (Carrying I mark))
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Short answer type questions)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View SolutionA coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is :
View Solution
Knowledge Check
A rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the
 Amagnetic field is increased uniformlyBmagnetic field is switched offCcoil is rotated about the axis XX'Dcoil is rotated about an axis perpendicular to the plane of the coil and passing through its centre )
Amagnetic field is increased uniformlyBmagnetic field is switched offCcoil is rotated about the axis XX'Dcoil is rotated about an axis perpendicular to the plane of the coil and passing through its centre )A straight conductor is placed along the axis of a circular coil perpendicular to the plane of the coil. Then electric current is passed through both,
Aonly straight conductor experiences forceBonly coil experiences forceCboth experience forceDnone experiences forceCurrent I is flowing through a circular coil of radius r. It is placed in a magnetic field B0 in such a way that the plane of the circular coil is perpendicular to B0. The force acting in it will be -
AπIrB0BIrB0CzeroD2πIrB0
A circular coil carrying current is placed in a region of uniform magnetic field acting perpendicular to the plane of the coil as shown in figure. The correct choice among the following is

View SolutionCurrent I is flowing through a circular coil of radius r. It is placed in a magnetic field B in such a way that the plane of the circular coil is perpendicular to B. The force acting on it will be -
View SolutionFigure-5.55 shows a small circular coil of area A suspended from a point O by a string of length l in a uniform magnetic induction B in a uniform magnetic induction B in horizontal direction. If the coil is set into oscillation like a simple pendulum by displacing it a small angle 00 as shown, find EMF induced in coil as a function of time. Assume the plane of coil is always in plane of string.
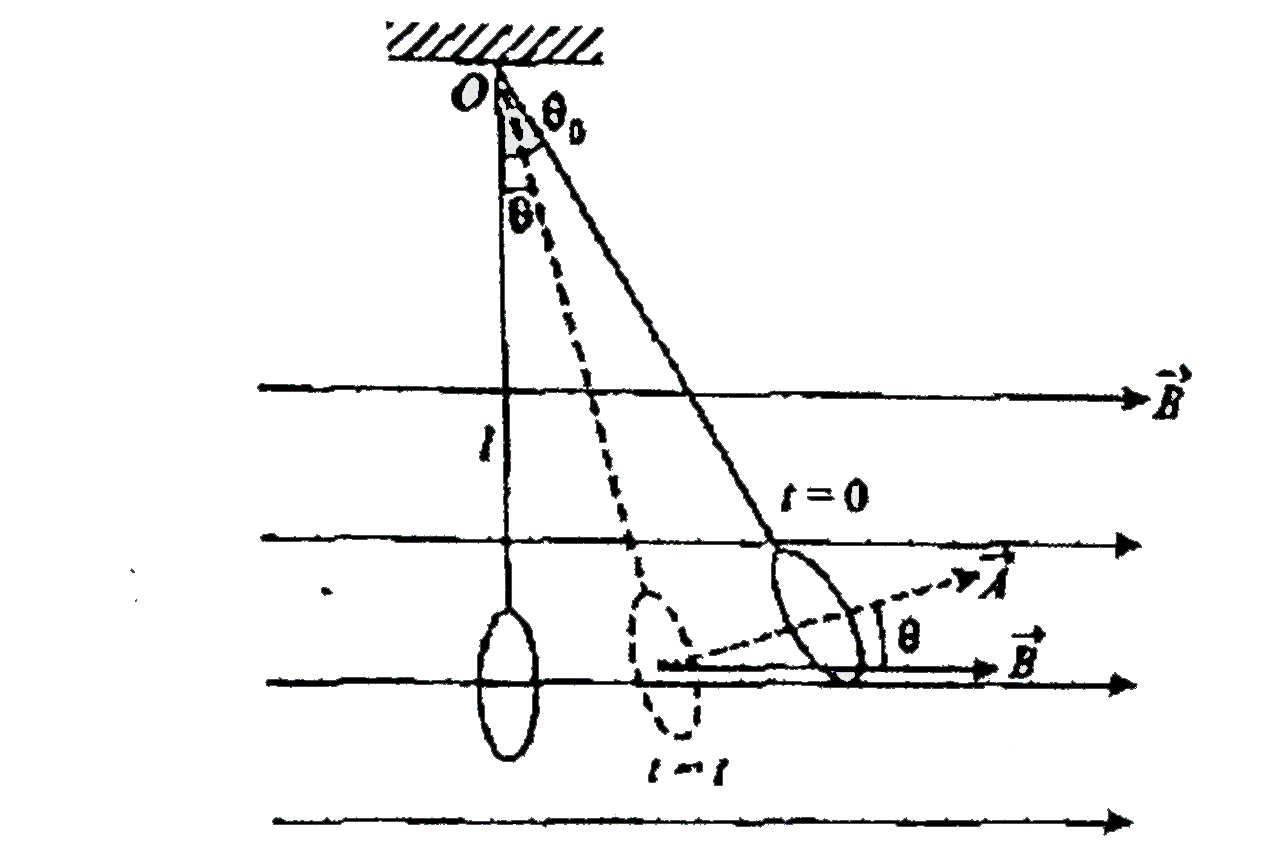
View SolutionA circular coil of radius r is placed in a uniform magnetic field B. The magnetic field is normal to the plane of the coil is rotated at an angular speed of ω, about its own axis , then the induced emf in the coil is __
View SolutionAn arbitrary shaped closed coil is made of a wire of length L and a current I ampere is flowing in it. If the plane of the coil is perpendicular to magnetic field →B, the force on the coil is
View Solution
