Light wave is travelling along X-axis in a medium. Which of the following can represent wavefront for this light wave ?
x=0
x=c
x2+y2+z2=c2
z=c
The correct Answer is:A, B
To solve the question regarding the representation of wavefronts for a light wave traveling along the X-axis in a medium, we can follow these steps:
Step 1: Understanding Wavefronts
A wavefront is defined as the surface over which an oscillation (such as a light wave) has a constant phase. For a light wave traveling in a particular direction, the wavefronts are perpendicular to the direction of propagation.
Step 2: Direction of Propagation
Since the light wave is traveling along the X-axis, we need to identify the plane that is perpendicular to this direction. The direction of propagation is along the X-axis, which means the wavefronts will be in a plane that is perpendicular to the X-axis.
Step 3: Identifying the Perpendicular Plane
The plane that is perpendicular to the X-axis can be represented by the YZ-plane. This is because any point in the YZ-plane has an X-coordinate of 0, meaning it does not change as we move in the Y and Z directions.
Step 4: Equations of the YZ-plane
The equations that represent the YZ-plane are:
- x=0 (this represents the plane where the X-coordinate is zero)
- x=c (this represents another plane parallel to the YZ-plane at a distance 'c' along the X-axis)
Conclusion
Therefore, the wavefronts for the light wave traveling along the X-axis can be represented by the equations:
- x=0
- x=c
Final Answer
The correct representations of the wavefront for the light wave traveling along the X-axis are x=0 and x=c.
---
A wavefront is defined as the surface over which an oscillation (such as a light wave) has a constant phase. For a light wave traveling in a particular direction, the wavefronts are perpendicular to the direction of propagation.
Since the light wave is traveling along the X-axis, we need to identify the plane that is perpendicular to this direction. The direction of propagation is along the X-axis, which means the wavefronts will be in a plane that is perpendicular to the X-axis.
The plane that is perpendicular to the X-axis can be represented by the YZ-plane. This is because any point in the YZ-plane has an X-coordinate of 0, meaning it does not change as we move in the Y and Z directions.
The equations that represent the YZ-plane are:
- x=0 (this represents the plane where the X-coordinate is zero)
- x=c (this represents another plane parallel to the YZ-plane at a distance 'c' along the X-axis)
Therefore, the wavefronts for the light wave traveling along the X-axis can be represented by the equations:
- x=0
- x=c
The correct representations of the wavefront for the light wave traveling along the X-axis are x=0 and x=c.
Topper's Solved these Questions
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)
Explore 7 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS)
Explore 10 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:OBJECTIVE TYPE QUESTIONS (JEE (ADVANCED) FOR IIT ENTRANCE)
Explore 6 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
Knowledge Check
Light waves travel in vacuum along the y-axis. Which of the following may represent the wavefront?
Ax = constantBy = constantCz = constantDx+y+z = constantWhich of the following represent a travelling wave ?
A(x−vt)2Bln(x+vt)Ce−(x−vt)2D1x+vtLight waves travel in vacuum along the y-axis. Which of the following may represent the wavefront?
Ay = constantBx = constantCt = constantDx+y+z= constant
Fig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.
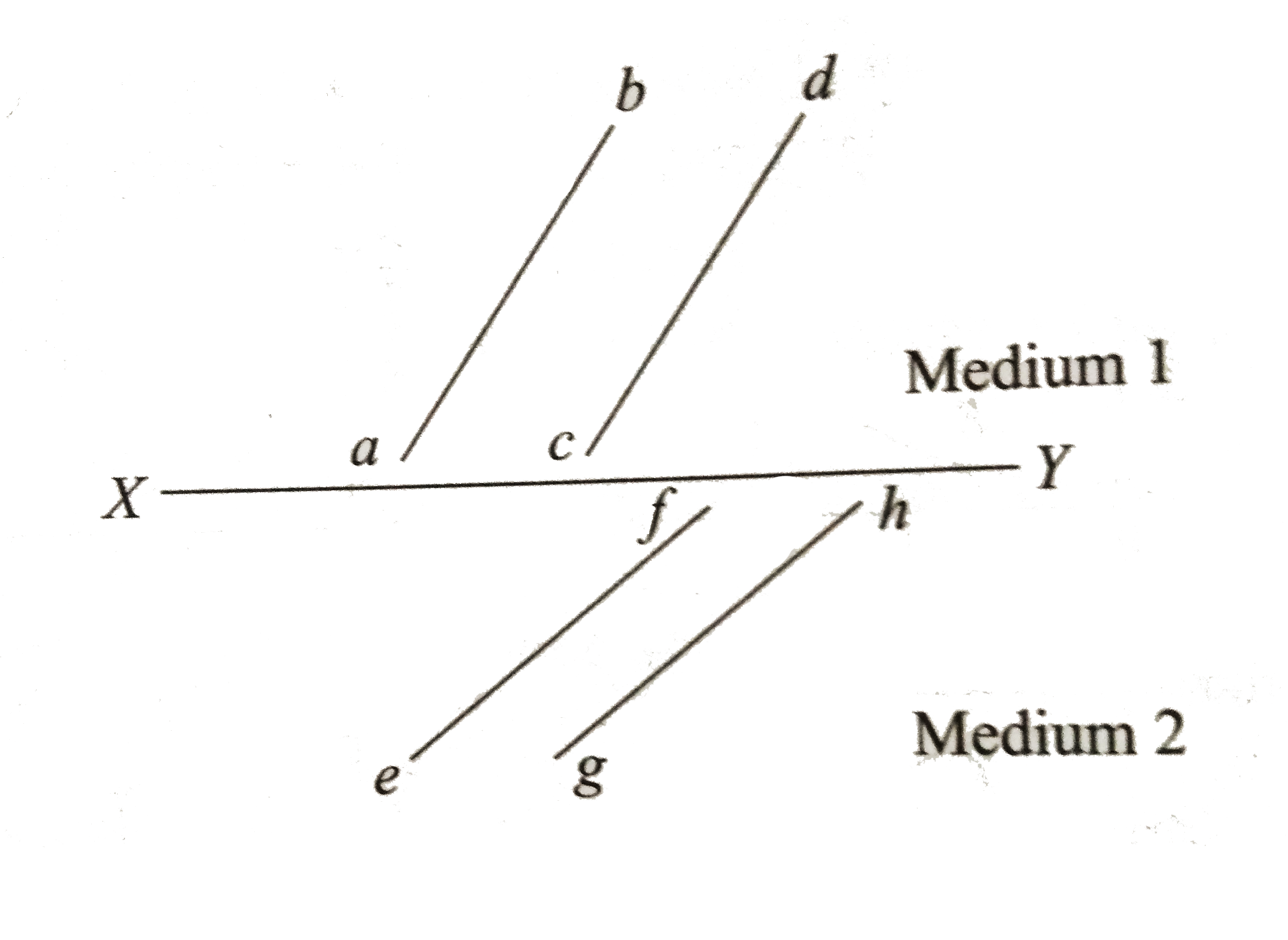 Speed of light is
Speed of light is
View SolutionThe figure shows a surface XY separating two transparent media, medium - 1 and medium - 2. The lines ab and cd represent wavefronts of the light ab and cd represent wavefronts of the light wave travelling in medium-1 and incident on XY. The lines of ef and gh represent wavefronts of the light wave in medium - 2 after refraction.

Answer the following question :
Light travels as a :
View SolutionThe figure shows a surface XY separating two transparent media, medium - 1 and medium - 2. The lines ab and cd represent wavefronts of the light ab and cd represent wavefronts of the light wave travelling in medium-1 and incident on XY. The lines of ef and gh represent wavefronts of the light wave in medium - 2 after refraction.

Answer the following question :
Speed of light is:
View SolutionThe figure shows XY separating two transparent media, medium-1 and medium-2. The lenes ab and cd represent wavefronts of a light wave travelling in medium-1 and incident on XY. The lines rf and gh represent wavefronts of the light wave in medium-2 after refraction.

The phases of the light wave at c,d,e and f are ϕc,ϕd,ϕe and ϕf respectively. It is given that ϕc=ϕf :
View SolutionWhich of the following equations represents a travelling wave?
View Solution