Two sources S1andS2 are shown in the figure. Refractive index of water is 4/3. Wavelength of light in air is λ.
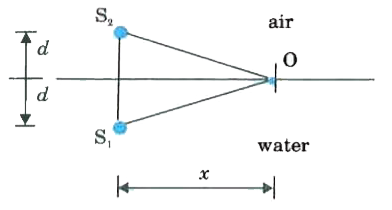
Minimum value of x so that there is maximum intensity at Point O is given by following relation:
x2=kλ2−d2
What is value of k ?
0123456789
The correct Answer is:9
Optical path difference between two waves reaching point, O should be integral multiple of wavelength for maxima, hence we can write the following equation:
μ√d2+x2−√d2+x2=mλ
⇒(μ−1)√d2+x2=mλ
⇒(43−1)√d2+x2=mλ
⇒d2+x2=9m2λ2
For minimum value of x we can substitute m = 1 and rewrite the above equation as follows:
x2=9λ2−d2
On comparing with the given expression we get k = 9.
Topper's Solved these Questions
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - CHAPTER PRACTICE TEST
7 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS)
1 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A Young's double-slit interference arrangement with slits S1andS2 is immersed in water (refractive index = 4/3) as shown in the figure. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (refractive index = 1), 2d is the separation between the slits and m is an interger. The value of p is

0123456789
View SolutionTwo light sources of intensities I and 4I are used to make interference pattern on a screen. What will be ratio of maximum to minimum intensity on the screen ?
0123456789
View Solution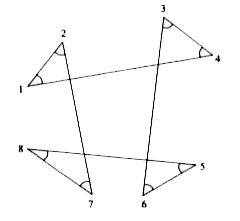
Angles are shown in the given figure. What is value of ∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8 ?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is

View SolutionLet two points be A(1,-1) and B(0,2) .If a point P(h,k) be such that the area of triangle PAB is 5 sq units and it lies on the line 3x+y-4 λ=0 ,then the value of λ is
View SolutionLet two points be A(1,−1) and B(0,2) .If a point P(h,k) be such that the area of ΔPAB=5 sq units and it lies on the line 3x+y−4λ=0 then a value of λ is
View SolutionIf x=−1 and x=15 are solutions of the equations x2+kx+λ=0. Find the value of k and λ
View SolutionA Young's double slit interference arrangement with slits S1 and S2, where S2 is immersed in water (refractive index =4/3). Surface of water is exactly between the two slits. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........

View SolutionA Young's double slit interference arrangement with slits S1 and S2 is immersed in water (refractive index =4/3) as shown in the figure. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........

View SolutionThe value of λ in order that the equations 2x2+5λx+2=0 and 4x2+8λx+3=0 have a common root is given by
View Solution
