A uniform disc of radius R and mass M is rotating about its rim on a horizontal surface of a table. Now the disc is pulled, with a force F acting on the centre of disc. What is the maximum value of F for which the disc rolls without slipping ? (μ = coeff, of frictoin)

F≤3μMg
F=2μMg
F≤4μMg
None of these
The correct Answer is:A
Let .f. be the force of friction. Then .a. be the acceleration of C.M. The equation of motion for the disc will be

Ma=F−f …(i)
If .a. is the angular acceleration then a=aR
But torque formed by .f. is τ=I.αorIα=f.R
12MR2.α=f.R
or12MR2.aR=f.R
or Ma = 2f Putting in (i)
F = 3f or f = F/3
As there is no sliding
∴f≤μmgandF≤3μmg
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - LEVEL-III (MCQ)
10 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- RAY OPTICSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION
32 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test
28 Videos
Similar Questions
A unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is spulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?


View SolutionA horizontal force F acts at the centre of mass of a uniform disc with mass M and radius R. The maximum value of F for which the disc can roll without slipping is kμsMg. Find k. ( μ, is coefficient of friction)
View Solution
Knowledge Check
A unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is pulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?

 AμMgB2μMgC3μMgD4μMg
AμMgB2μMgC3μMgD4μMgA uniform disc of radius R and mass M can rotate on a smooth axis passing through its centre and perpendicular to its plane. A force F is applied on its rim. See fig. What is the tangential acceleration
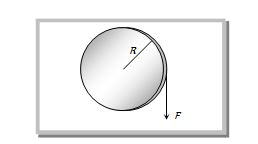 A2FMBFMCF2MDF4M
A2FMBFMCF2MDF4MA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
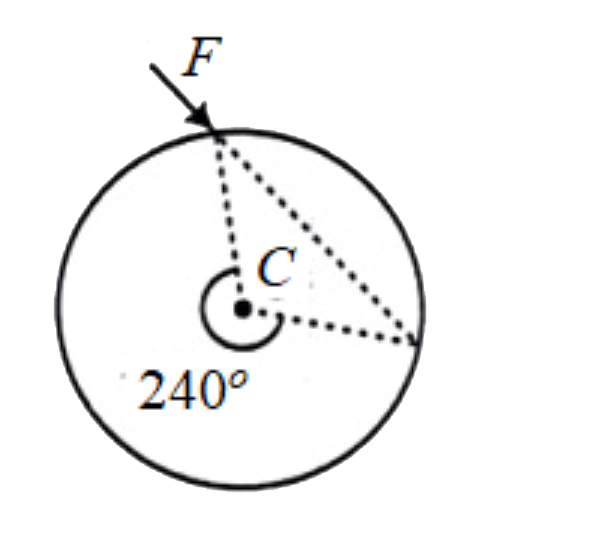 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MR
A circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
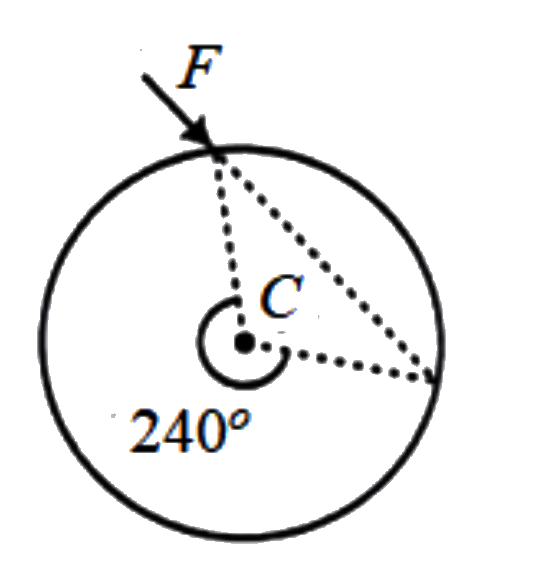
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

View Solution
