A ring of radius 4a is rigidly fixed vertically on the horizontal surface of a table. A small disc of radius 'a' and mass 'm' is released from point P of the ring as shown. The disc rolls down without slipping to the lower most position A of the ring the speed of disc at this point is :

(ga)1/2
(2ga)1/2
(3ga)1/2
(4ga)1/2
The correct Answer is:D
Applying the law of conservation of energy mgh = Energy of translation + Energy of rotation
mgh=12mv2+12Iω2
=12mv2[1+k2R2]
mg×3a=12mv2×3/2
v2=4gaorv=(4ga)1/2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - LEVEL-III (MCQ)
10 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- RAY OPTICSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION
32 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test
28 Videos
Similar Questions
Knowledge Check
A ring of radius 4a is rigidly fixed in vertical position on a table. A small disc of mass m and radius a is released as shown in the fig. When the disc rolls down, without slipping, to the lowest point of the ring, then its speed will be
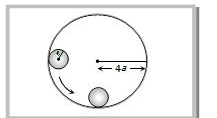 A√gaB√2gaC√3gaD√4ga
A√gaB√2gaC√3gaD√4gaA ring of mass M and radius R is at rest at the top of an incline as shown. The ring rolls down the plane without slipping. When the ring reaches bottom, its angular momentum about its centre of mass is:
 AMR√ghBMR√gh2CMR√2ghDnone
AMR√ghBMR√gh2CMR√2ghDnoneA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is
 A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj
A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj
A disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

View SolutionA disc is in the condition of pure rolling on the horizontal surface. The velocity of center of mass isV0 If radius of disc is R then the speed of point P is (OP=R3)
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

View Solution


