When two progressive waves y1 = 4 sin (2x - 6t) and y2=3sin(2x−6t−π2) are superimposed, the amplitude of the resultant wave is ............. .Solution in Kannada
5 m
10 m
20 m
40 m
The correct Answer is:B
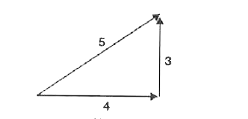
since Δϕ=π/2 ,
Aresultant =(A21+A22+2A1A2cosΔϕ)1/2
=√(4)2+(3)2 = 5
So, correct choice is (b) .
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE MOTIONEXERCISE - MULTIPLE CHOICE QUESTIONS (LEVEL -II)73videos
WAVE MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE MOTIONEXERCISE - MULTIPLE CHOICE QUESTIONS (LEVEL -III)8videos
WAVE MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - UNITS, MEASURMENTS, DIMENSIONS, ERRORS OF MEASUREMENTSEXERCISE - Recent Competitive Questions7videos
UNITS, MEASURMENTS, DIMENSIONS, ERRORS OF MEASUREMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - Recent Competitive Questions18videos
WAVE OPTICS
Similar Questions
A stone is dropped into a well and sound of impact of stone with water is heard after 2.056 second of the release of stone from top If g 980 cm/s2 and velocity of sound is 350 m/s. Then depth of well is :
01:20View SolutionThe transverse displacement y(x,t) of a wave on a string is given by y (x,t) = e−(ax2+bt2+2√abxt) . This represents a :
02:10View SolutionThe dimensions of 'resistance' are same as those of . . . . . . . . . Where h is the Planck's constant e is the charge .
02:11View SolutionThe wavelength of the light used in Young's double slit experiment is λ.The intensity at a point on the screen is I, where the path difference is λ6. If I0 denotes the maximum intensity, then the ratio of I and I0 is :
04:34View SolutionWhen two progressive waves y1=4sin(2x−6t) and y2=3sin(2x−6t−π2) are superimposed, the amplitude of the resultant wave is
02:29View SolutionThe mathmaticaly form of three travelling waves are given by Y_(1)=(2 cm) sin (3x-6t) Y_(2)=(3 cm) sin (4x-12t) And Y_(3)=94 cm) sin(5x-11t) of these waves,
03:07View SolutionTwo waves y1=A1sin(ωt−β1),y2=A2sin(ωt−β2) Superimpose to form a resultant wave whose amplitude is
04:24View SolutionThe equations for displacement of two light waves forming interference pattern are y_(1) = 4 sin omega t and y_(2) =3 sin (omega t+ (pi)/(2)) . Determine the amplitude of the resultant wave.
03:09View SolutionEquations of two light waves are y1= 4 sin ω t and y2=3sin(ωt+π2). What is the amplitude of the resultant wave as they superpose on each other?
View SolutionThe displacement of two interfering light waves are given by y1=3sinωt,y2=4sin(ωt+π/2). The amplitude of the resultant wave is
03:00View Solutionजब दो प्रगामी तरंगे y1=4sin(2x−6t) तथा y2=3sin(2x−6t−π2) अध्यारोपित होती है तो परिणामी तरंग का आयाम कितना होगा ?
07:36View SolutionWhen two progressive waves y1=4sin(2x−6t)andy2=3sin(2x−6t−π2) are superposed, the amplitude of the resultant wave is
View SolutionTwo waves given by y_(1)=asinomegat and y_(2)=a sin (omegat+pi//2) reaching at a point superimpose. The resultant amplitude is
03:00View SolutionThe displacement of two interfering light waves are y1=4sinωt and y2=3cosωt. The amplitude of the resultant wave is (y1 and y2 are in CGS system)
02:30View Solutiony1=4sinωt तथा y2=3sin(ωt+π2) तरंगो के अध्यारोपण से बनने वाली तरंग का परिणामी आयाम होगा
02:55View Solution

