Question

If the area bounded by the curve $y=x^2+1$
and the tangents to it drawn from the origin is $A,$
then the value of $3A$
is__-

Answer

2

Explanation

Let the point of the curve be `(x,x^(2)+1).`
Now, the slope of tangent at this point is 2x, which is equal to the slope of the line joining `(x,x^(2)+1) and (0,0).`
`"Hence, "2x=(x^(2)+1)//x or 2x^(2)=x^(2)+1`
`"or "x^(2)+1 or x=pm1`

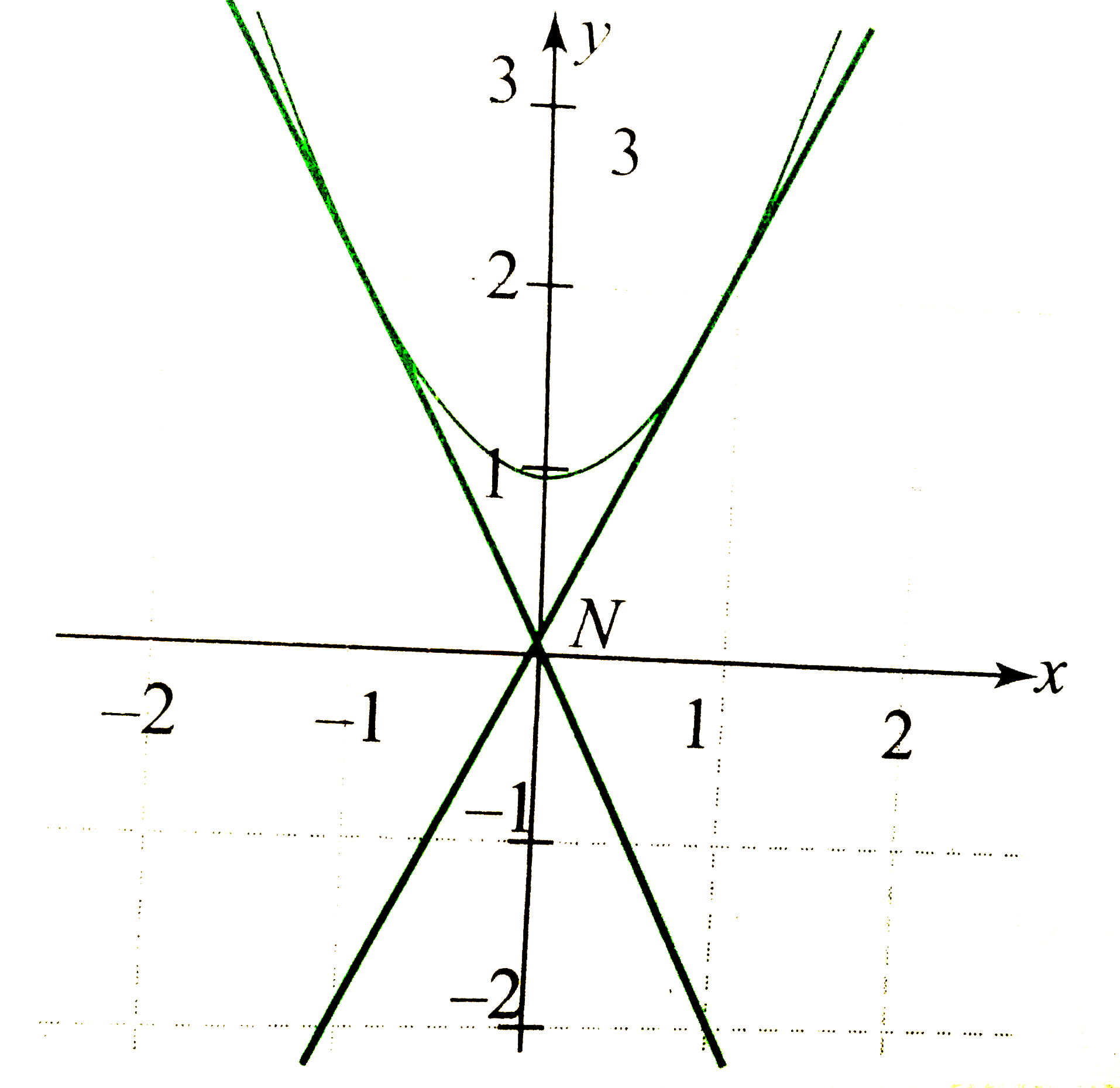
Hence, equation of tangent is `y=pm2x`
`"Now Area "2overset(1)underset(0)int(x^(2)+1-2x)dx=2overset(1)underset(0)int(x-1)^(2)dx=2[(x-1)^(3)/(3)]_(0)^(1)=2//3`