If $A$ is the area bounded by the curves $y = \sqrt{1 - x^{2}}$ and $y = x^{3} - x$ , then of $\frac{π}{A} .$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

$y = \sqrt{1 - x^{2}} (1)$
$y = x^{3} - x (2)$
$y = 0 in (2) x = 0, 1, - 1$

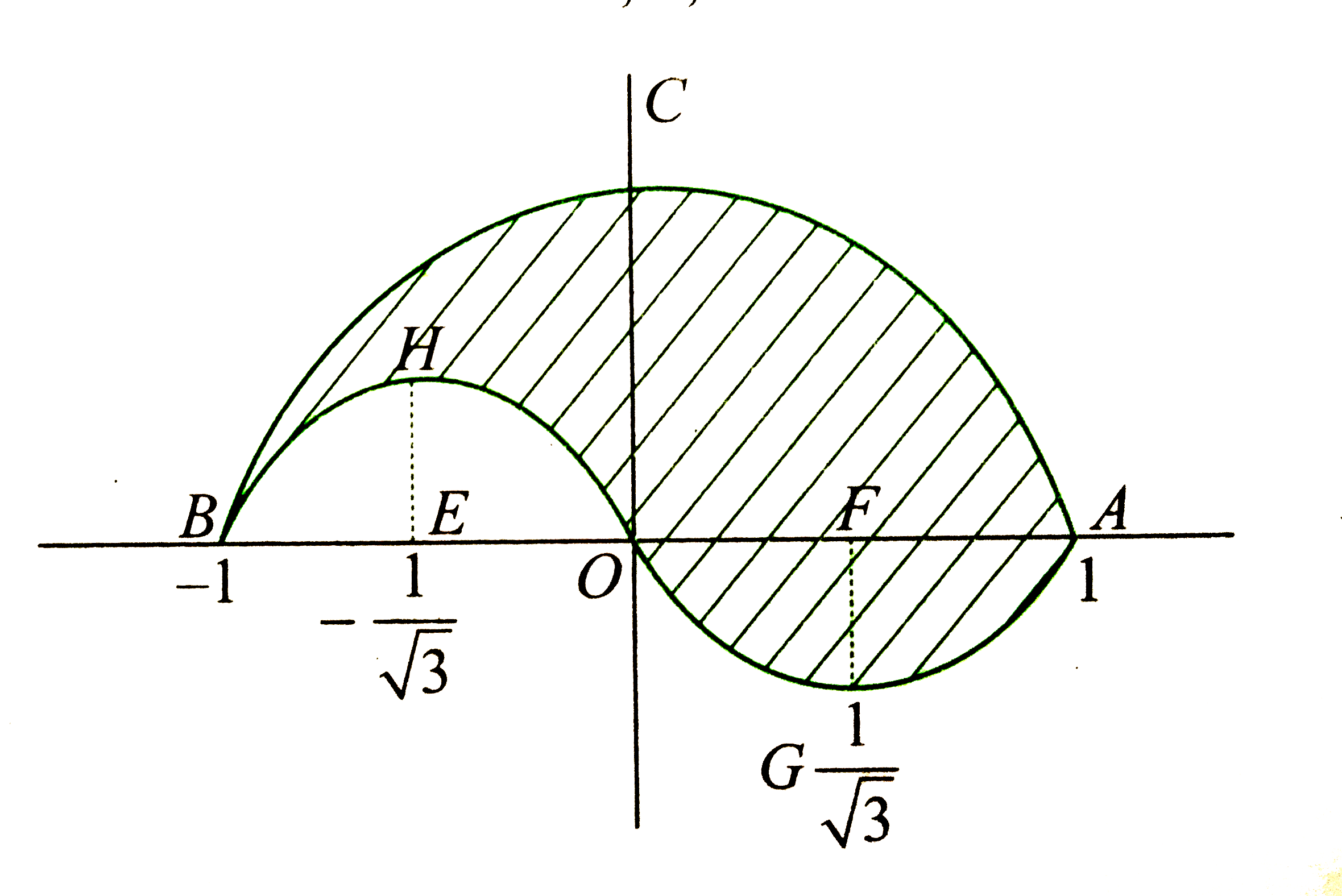
Required area = Area of region BCAGOHB
=Area of semi-circle BCAOB
$= \frac{π}{2} (∵ area of BHOEB= area of OFAGO)$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year
10videos
AREA
BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9videos
AREA
BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4videos
AREA
BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29videos
APPLICATIONS OF DERIVATIVES
BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20videos
AREA UNDER CURVES

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the curves $y = \sqrt{5 - x^{2}}$ and $y = | x - 1 |$ is
A $(\frac{5 π}{4} - 2)$ sq units
B $(\frac{5 π - 2}{4})$ sq units
C $(\frac{5 π - 2}{2})$ sq units
D $(\frac{π}{2} - 5)$ sq units
Question 2 - Select One
The area bounded by the curves $y = x^{3}$ and y = x is
A $1 / 2$ sq unit
B $1 / 4$ sq unit
C $1 / 8$ sq unit
D $1 / 16$ sq unit
Question 3 - Select One
The area bounded by the curves $y = - x^{2} + 3 and y = 0$ is
A $\sqrt{3} + 1$
B $\sqrt{3}$
C $4 \sqrt{3}$
D $5 \sqrt{3}$

CENGAGE-AREA-Exercise (Numerical)

Home
Ask Doubt
Profile