If the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2} is A , then the value of 3A−17 is____
Video Solution
Text Solution
The correct Answer is:6
Draw the given region point of intersection of y=x2+1
y=x+1
x+1=x2+1
x=0,1
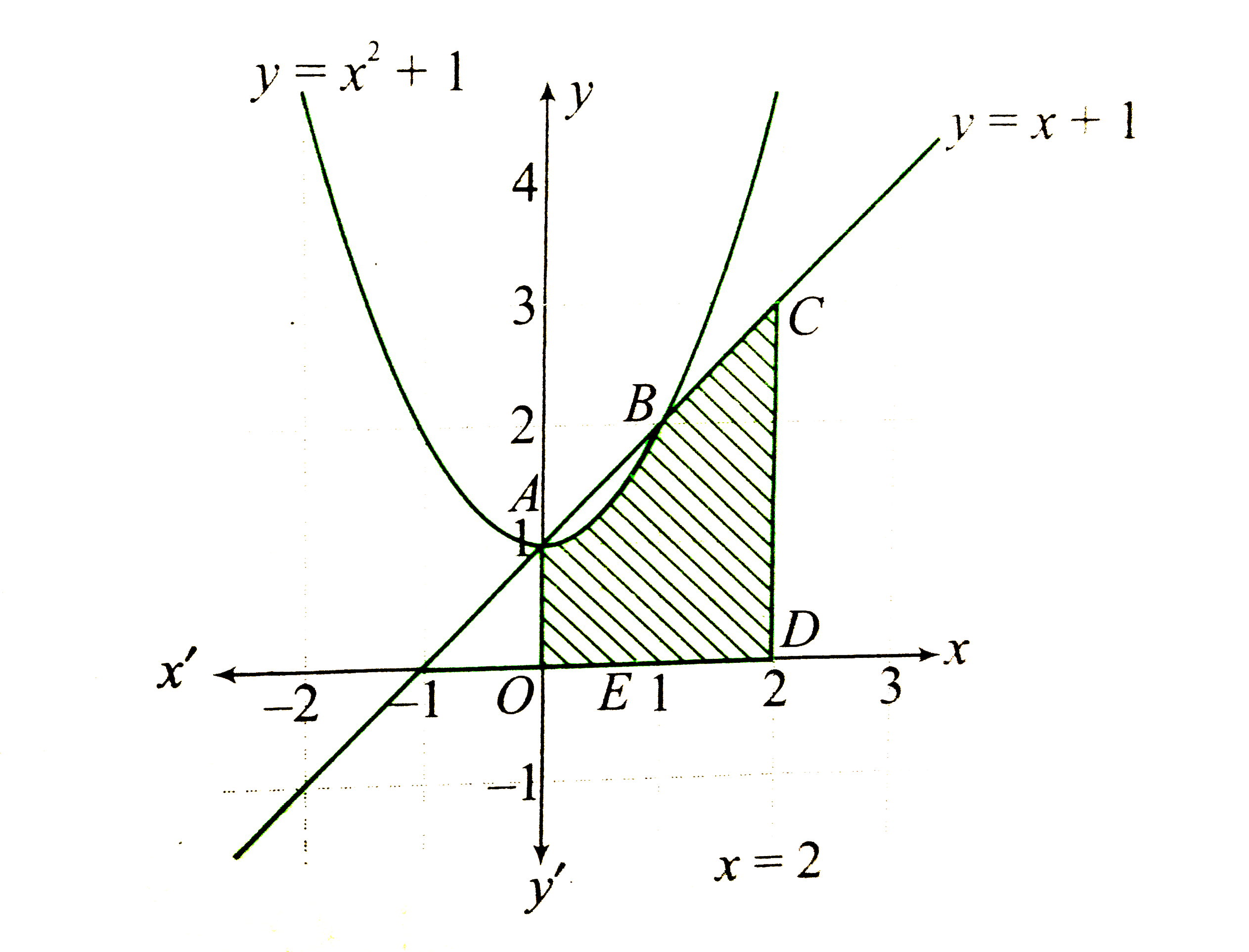
Required area OABCDE=1∫0(x2+1)dx+2∫1(x+1)dx
=(x33+x)10+(x22+x)21=236 sq. units
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year9videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)4videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Knowledge Check
- Question 1 - Select One
x2+1<0
A−1≤x≤1B−1<x<0CDoes not existDnone of these - Question 2 - Select One
The area of the region for which o<y<3−2x−x2 and x>0, is
A3∫1(3−2x−x2)dxB3∫0(3−2x−x2)dxC1∫0(3−2x−x2)dxD3∫−1(3−2x−x2)dx - Question 3 - Select One
If [] denotes the greatest integer less than or equal to the real number under consideration and −1≤x<0,0≤y<1,1≤z<2, the value of the determinant ∣∣ ∣ ∣∣[x]+1[y][z][x][y]+1[z][x][y][z]+1∣∣ ∣ ∣∣ is
A[x]B[y]C[z]DNone of these
Let f:[0, ∞)→R be a continuous function such that f(x)=1−2x+∫x0ex−tf(t)dt for all x∈[0, ∞) . Then, which of the following statement(s) is (are) TRUE? The curve y=f(x) passes through the point (1, 2) (b) The curve y=f(x) passes through the point (2, −1) (c) The area of the region {(x, y)∈[0, 1]×R:f(x)≤y≤√1−x2} is π−24 (d) The area of the region {(x, y)∈[0, 1]×R:f(x)≤y≤√1−x2} is π−14
View SolutionIf α,β are the roots of x2−3x+a=0,a∈Rand<1<β,
then find the values of aView SolutionIf tanx=1,0<x<90∘, then what is the value of 2 sin x cos x?
View SolutionIf (sin−1x)2−(cos−1x)2=a , 0<x<1, a≠0, then the value of 2x2−1 is
View SolutionIf x<0<y, then :
View Solution

