Area bounded by the curve where denotes the greatest integer function
Video Solution
Text Solution
The correct Answer is:3
Similarly we can consider
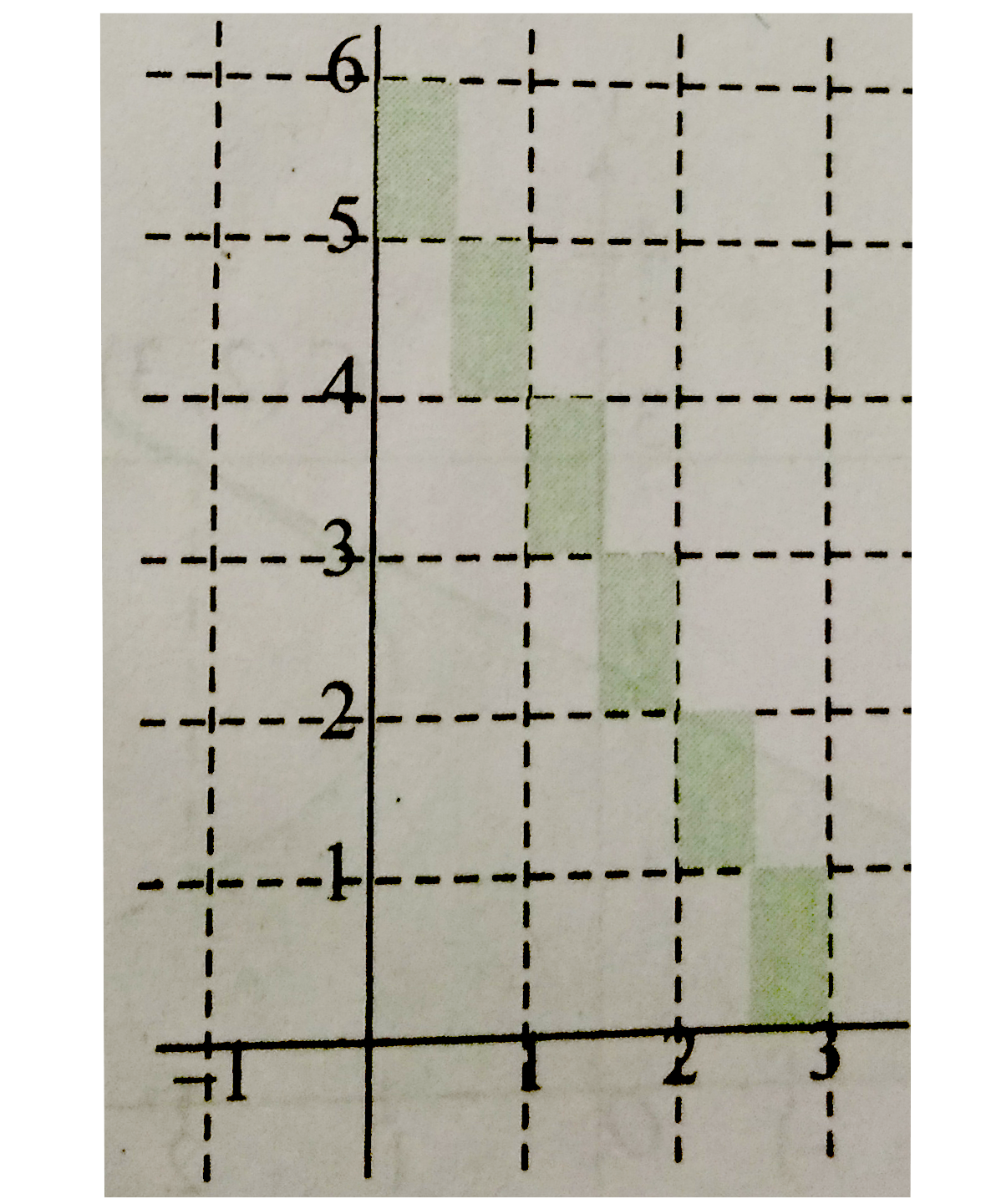
From the graph, area is 3 sq. units
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year9videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)4videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Knowledge Check
- Question 1 - Select One
Let f(x) =[x]2+[x+1]−3, where [.] denotes the greatest integer function. Then
Af(x)≠0 for all real values of xBf(x) = 0 for only two real value of xCf(x) = 0 for infinite values of x.Df(x) = 0 for no real value of x
Draw the graph of y=[|x|], where [.] denotes the greatest integer function.
View SolutionSolve in R: x2+2[x]=3x where [.] denotes greatest integer function.
View SolutionFind the area enclosed by the curve [x]+[y]−4 in 1st quadrant (where [.] denotes greatest integer function).
View SolutionArea enclosed by [|x|][|y|]=2,−5≤x≤5 is (where [.] denotes the greatest integer function)
View SolutionArea of the region bounded by [x]2=[y]2 ,if x∈[1,3] (where [ .] denotes the greatest integer function),is less than
View SolutionSketch the curves
(ii) y=[x]+√x−[x]
(where [.] denotes the greatest integer function).View SolutionSketch the curves
(i)y=√x−[x]
(where [.] denotes the greatest integer function).View Solution

