Draw the graph of the relation $y^{2} = x^{2} (1 - x)$

Text Solution

Verified by Experts

We have $y^{2} = x^{2} (1 - x)$
$\Rightarrow y = \pm x \sqrt{1 - x}$
Let us first draw the graph of $y = f (x) = x \sqrt{1 - x}$ .
This function is defined if $x \leq 1$
For $0 < x \leq 1, y > 0$ and for $x < 0, y < 0$
Also $y = 0 \Rightarrow x = 0, 1$
When $x \to - \infty, y \to - \infty$
$f^{'} (x) = (1 . \sqrt{1 - x} - \frac{x}{2 \sqrt{1 - x}})$
$\frac{2 - 3 x}{2 \sqrt{1 - x}}$
$f^{'} (x) = 0 ∴ x = \frac{2}{3}$ , which is the point of maxima.
Thus, graph of the function is as shown in the adjacent figure.

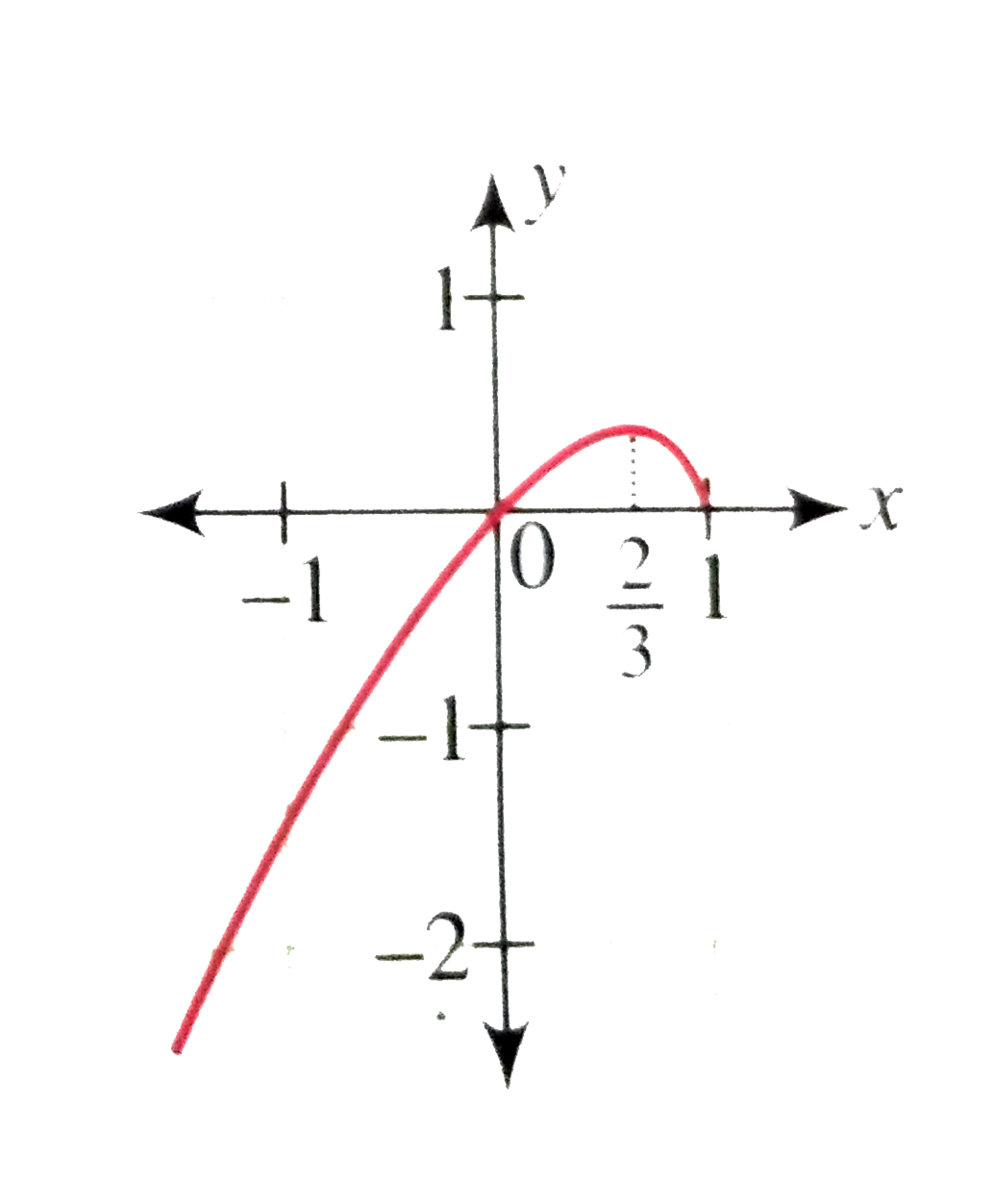
To draw the graph of $y = - x \sqrt{1 - x}$ , reflect the graph above the graph in the x-axis. Hence the graph of the relation $y^{2} = x^{2} (1 - x)$ is as shown in the following figure.

Updated on:21/07/2023

|

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

CENGAGE-CURVE TRACING-Exercise

Home
Ask Doubt
Profile